题目内容
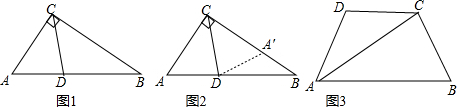
2.阅读下面材料:小明遇到这样一个问题:如图1,在Rt△ABC中,∠ACB=90°,∠A=60°,CD平分∠ACB,试判断BC和AC、AD之间的数量关系.
小明发现,利用轴对称做一个变化,在BC上截取CA′=CA,连接DA′,得到一对全等的三角形,从而将问题解决(如图2).
请回答:
(1)在图2中,小明得到的全等三角形是△ADC≌△A′DC;
(2)BC和AC、AD之间的数量关系是BC=AC+AD.
参考小明思考问题的方法,解决问题:
如图3,在四边形ABCD中,AC平分∠BAD,BC=CD=10,AC=17,AD=9.求AB的长.
分析 (1)由SAS容易证明△ADC≌△A′DC;
(2)由△ADC≌△A′DC,得出DA′=DA,∠CA′D=∠A=60°,再求出DA′=BA′,得出BA′=AD,即可得出结论;
解决问题:在AB上截取AE=AD,连接CE,先证明△ADC≌△AEC,得出AE=AD=9,CE=CD=10=BC,过点C作CF⊥AB于点F,设EF=BF=x;在Rt△CFB和Rt△CFA中,根据勾股定理求出x,即可得出结果.
解答 解:(1)△ADC≌△A′DC;理由如下:
∵CD平分∠ACB,
∴∠ACD=∠A′CD,
在△ADC和△A′DC中,
$\left\{\begin{array}{l}{CA′=CA}&{\;}\\{∠ACD=∠A′CD}&{\;}\\{CD=CD}&{\;}\end{array}\right.$,
∴△ADC≌△A′DC(SAS);
(2)BC=AC+AD;理由如下:
由(1)得:△ADC≌△A′DC,
∴DA′=DA,∠CA′D=∠A=60°,
∵∠ACB=90°,
∴∠B=90°-∠A=30°,
∵∠CA′D=∠B+∠BDA′,∠∠BDA′=30°=∠B,
∴DA′=BA′,
∴BA′=AD,
∴BC=CA′+BA′=AC+AD;
解决问题
如图,在AB上截取AE=AD,连接CE,如图3所示: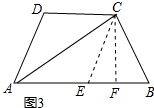
∵AC平分∠BAD,
∴∠DAC=∠EAC.
在△AEC和△ADC中,
$\left\{\begin{array}{l}{AE=AD}&{\;}\\{∠DAC=∠EAC}&{\;}\\{AC=AC}&{\;}\end{array}\right.$,
∴△ADC≌△AEC(SAS),
∴AE=AD=9,CE=CD=10=BC,
过点C作CF⊥AB于点F,
∴EF=BF,
设EF=BF=x.
在Rt△CFB中,∠CFB=90°,由勾股定理得CF2=CB2-BF2=102-x2,
在Rt△CFA中,∠CFA=90°,由勾股定理得CF2=AC2-AF2=172-(9+x)2.
∴102-x2=172-(9+x)2,
解得:x=6,
∴AB=AE+EF+FB=9+6+6=21,
∴AB的长为21.
点评 本题考查了全等三角形的判定与性质、勾股定理、等腰三角形的判定与性质;本题有一定难度,需要通过作辅助线证明三角形全等才能得出结果.

 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案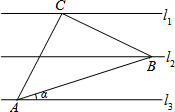 如图,已知l1∥l2∥l3,相邻两条平行直线间的距离相等,若等腰直角△ABC的直角顶点C在l1上,另两个顶点A、B分别在l2、l3上,则tanα的值是( )
如图,已知l1∥l2∥l3,相邻两条平行直线间的距离相等,若等腰直角△ABC的直角顶点C在l1上,另两个顶点A、B分别在l2、l3上,则tanα的值是( )| A. | $\frac{1}{3}$ | B. | $\frac{6}{17}$ | C. | $\frac{{\sqrt{5}}}{5}$ | D. | $\frac{{\sqrt{10}}}{10}$ |
| A. | 了解在校大学生的主要娱乐方式 | |
| B. | 了解“嫦娥三号”卫星零部件的状况 | |
| C. | 日光灯管厂要检测一批灯管的使用寿命 | |
| D. | 了解某市居民对废电池的处理情况 |
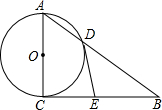 如图,以Rt△ABC的直角边AC为直径的圆⊙O交斜边AB于点O,过D作⊙O的切线DE,交CB于E.
如图,以Rt△ABC的直角边AC为直径的圆⊙O交斜边AB于点O,过D作⊙O的切线DE,交CB于E.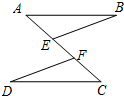 如图,点E,F在线段AC上,AB∥CD,AB=CD,AE=CF.求证:BE=DF.
如图,点E,F在线段AC上,AB∥CD,AB=CD,AE=CF.求证:BE=DF.
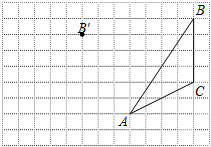 画图并填空:如图,方格纸中每个小正方形的边长都为1.在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.利用网格点和三角板画图或计算:
画图并填空:如图,方格纸中每个小正方形的边长都为1.在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.利用网格点和三角板画图或计算: