题目内容
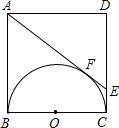 在边长为a的正方形内ABCD中,AE与以BC为直径的半圆相切于点F,交CD于E,求CF、FD的长.
在边长为a的正方形内ABCD中,AE与以BC为直径的半圆相切于点F,交CD于E,求CF、FD的长.考点:切线的性质,正方形的性质
专题:计算题
分析:作FM⊥BC于M,交AD于N,连结BF、CF、DF、OE,CF与OE交于H,根据切线长定理得AF=AB=a,EF=EC,设EC=x,则EF=x,DE=a-x,AE=a+x,在Rt△AED中,利用勾股定理得AE2=AD2+DE2,可得到EC=
a,在Rt△OEC中,根据勾股定理计算得OE=
a,在利用面积法得
CH•OE=
OC•CE,可计算得CH=
a,利用垂径定理得CF=2CH=
a;在Rt△BCF中,根据勾股定理计算出BF=
a,再利用面积法计算出FM=
a,在Rt△FMC中,计算出MC=
a,则DN=MC=
a,NF=MN-MF=
a,然后利用勾股定理计算DF=
a.
| 1 |
| 4 |
| ||
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 10 |
| ||
| 5 |
2
| ||
| 5 |
| 2 |
| 5 |
| 1 |
| 5 |
| 1 |
| 5 |
| 3 |
| 5 |
| ||
| 5 |
解答:解:作FM⊥BC于M,交AD于N,连结BF、CF、DF、OE,CF与OE交于H,如图,
∵AB和AF是⊙O的切线,
∴AF=AB=a,
∵EF和EC是⊙O的切线,
∴EF=EC,
设EC=x,则EF=x,DE=a-x,AE=a+x,
在Rt△AED中,∵AE2=AD2+DE2,
∴(a+x)2=a2+(a-x)2,
∴x=
a,即EC=
a,
在Rt△OEC中,OE=
=
=
a,
∵
CH•OE=
OC•CE,
∴CH=
=
a,
∴CF=2CH=
a,
∵BC为直径,
∴∠BFC=90°,
在Rt△BCF中,BF=
=
a,
∵
BC•FM=
BF•CF,
∴FM=
a,
在Rt△FMC中,MC=
=
a,
∴DN=MC=
a,NF=MN-MF=a-
a=
a,
在Rt△DFN中,DF=
=
a,
∴CF、FD的长分别为
a,
a.
∵AB和AF是⊙O的切线,
∴AF=AB=a,

∵EF和EC是⊙O的切线,
∴EF=EC,
设EC=x,则EF=x,DE=a-x,AE=a+x,
在Rt△AED中,∵AE2=AD2+DE2,
∴(a+x)2=a2+(a-x)2,
∴x=
| 1 |
| 4 |
| 1 |
| 4 |
在Rt△OEC中,OE=
| OC2+CE2 |
(
|
| ||
| 4 |
∵
| 1 |
| 2 |
| 1 |
| 2 |
∴CH=
| ||||
|
| ||
| 10 |
∴CF=2CH=
| ||
| 5 |
∵BC为直径,
∴∠BFC=90°,
在Rt△BCF中,BF=
| BC2-CF2 |
2
| ||
| 5 |
∵
| 1 |
| 2 |
| 1 |
| 2 |
∴FM=
| 2 |
| 5 |
在Rt△FMC中,MC=
| CF2-FM2 |
| 1 |
| 5 |
∴DN=MC=
| 1 |
| 5 |
| 2 |
| 5 |
| 3 |
| 5 |
在Rt△DFN中,DF=
| DN2+NF2 |
| ||
| 5 |
∴CF、FD的长分别为
| ||
| 5 |
| ||
| 5 |
点评:本题考查了切线的性质:圆的切线垂直于经过切点的半径;经过圆心且垂直于切线的直线必经过切点;经过切点且垂直于切线的直线必经过圆心.也考查了正方形的性质和勾股定理.

练习册系列答案
相关题目


 如图,在平面直角坐标系xOy中,一次函数y=ax+b的图象与反比例函数
如图,在平面直角坐标系xOy中,一次函数y=ax+b的图象与反比例函数
 为了测量校园水平地面上一棵树的高度,数学兴趣小组利用一组标杆、皮尺,设计了如图所示的测量方案.已知测量同眼睛A标杆顶端F树的顶端E同一直线上,此同学眼睛距地面1.6m标杆长为3.3m且BC=1m,CD=4m,则ED=
为了测量校园水平地面上一棵树的高度,数学兴趣小组利用一组标杆、皮尺,设计了如图所示的测量方案.已知测量同眼睛A标杆顶端F树的顶端E同一直线上,此同学眼睛距地面1.6m标杆长为3.3m且BC=1m,CD=4m,则ED= 如图,点A、B、C在⊙O上,∠ACB=60°,则∠OAB的度数是
如图,点A、B、C在⊙O上,∠ACB=60°,则∠OAB的度数是 将一副三角板如图叠放,如OB=2
将一副三角板如图叠放,如OB=2