题目内容
 △ABC中,∠C=Rt∠,AC=3,BC=4,以点C为圆心,CA为半径的圆与AB、BC分别交于点E、D,则AE的长为( )
△ABC中,∠C=Rt∠,AC=3,BC=4,以点C为圆心,CA为半径的圆与AB、BC分别交于点E、D,则AE的长为( )A、
| ||
B、
| ||
C、
| ||
D、
|
考点:垂径定理,勾股定理
专题:
分析:在Rt△ABC中,由勾股定理可直接求得AB的长;过C作CM⊥AB,交AB于点M,由垂径定理可得M为AE的中点,在Rt△ACM中,根据勾股定理得AM的长,从而得到AE的长.
解答: 解:在Rt△ABC中,
解:在Rt△ABC中,
∵AC=3,BC=4,
∴AB=
=5.
过C作CM⊥AB,交AB于点M,如图所示,
由垂径定理可得M为AE的中点,
∵S△ABC=
AC•BC=
AB•CM,且AC=3,BC=4,AB=5,
∴CM=
,
在Rt△ACM中,根据勾股定理得:AC2=AM2+CM2,即9=AM2+(
)2,
解得:AM=
,
∴AE=2AM=
.
故选C.
 解:在Rt△ABC中,
解:在Rt△ABC中,∵AC=3,BC=4,
∴AB=
| 32+42 |
过C作CM⊥AB,交AB于点M,如图所示,
由垂径定理可得M为AE的中点,
∵S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
∴CM=
| 12 |
| 5 |
在Rt△ACM中,根据勾股定理得:AC2=AM2+CM2,即9=AM2+(
| 12 |
| 5 |
解得:AM=
| 9 |
| 5 |
∴AE=2AM=
| 18 |
| 5 |
故选C.
点评:本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
“二次函数y=ax2+bx+c的图象与x轴有两个公共点,那么一元二次方程ax2+bx+c=0有两个不相等的实数根.”请根据对这句话的理解,解决下面问题:若m,n(m<n)是关于x的方程2-(x-a)(x-b)=0的两根,且a<b,则a,b,m,n的大小关系是( )
| A、a<m<n<b |
| B、a<m<b<n |
| C、m<a<b<n |
| D、m<a<n<b |
把一个长方形划分成三个全等的长方形,若要使每一个小长方形与原长方形相似,则原长方形的长a与宽b的关系是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
2710-324可以被20和30之间的某两个整数整除,这两个数是( )
| A、22,24 |
| B、23,25 |
| C、26,28 |
| D、27,29 |

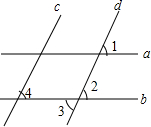 如图,已知a∥b,∠1=60°,∠4=60°,求∠3的度数并判断直线c,d的位置关系,请完善求解过程,并在括号内填上相应的依据.
如图,已知a∥b,∠1=60°,∠4=60°,求∠3的度数并判断直线c,d的位置关系,请完善求解过程,并在括号内填上相应的依据.