题目内容
8. 如图,在△ABC中,∠C=90°,sinB=$\frac{3}{5}$,AB=15,求△ABC的周长和tanA的值.
如图,在△ABC中,∠C=90°,sinB=$\frac{3}{5}$,AB=15,求△ABC的周长和tanA的值.
分析 根据题中所给的条件,在直角三角形中解题,根据角的正弦值与三角形边的关系及勾股定理,可求出各边的长,代入三角函数进行求解.
解答 解:在△ABC中,因为∠C=90°,$sinB=\frac{3}{5}$,AB=15,
所以$\frac{AC}{AB}$=$\frac{3}{5}$,即$\frac{AC}{15}$=$\frac{3}{5}$,
所以AC=9,
又因为AC2+BC2=AB2,
所以BC=12,
所以△ABC的周长AC+BC+AB=9+12+15=36,
$tanA=\frac{BC}{AC}=\frac{12}{9}=\frac{4}{3}$.
点评 本题考查了利用锐角三角函数和勾股定理解直角三角形的能力,还考查解直角三角形的定义,由直角三角形已知元素求未知元素的过程,还考查了直角三角形的性质.

练习册系列答案
相关题目
3. 如图,⊙O的直径CD=12cm,AB是⊙O的弦,AB⊥CD,垂足为E,OE:OC=1:3,则AB的长为( )
如图,⊙O的直径CD=12cm,AB是⊙O的弦,AB⊥CD,垂足为E,OE:OC=1:3,则AB的长为( )
 如图,⊙O的直径CD=12cm,AB是⊙O的弦,AB⊥CD,垂足为E,OE:OC=1:3,则AB的长为( )
如图,⊙O的直径CD=12cm,AB是⊙O的弦,AB⊥CD,垂足为E,OE:OC=1:3,则AB的长为( )| A. | 2$\sqrt{2}$cm | B. | 4$\sqrt{2}$cm | C. | 6$\sqrt{2}$cm | D. | 8$\sqrt{2}$cm |
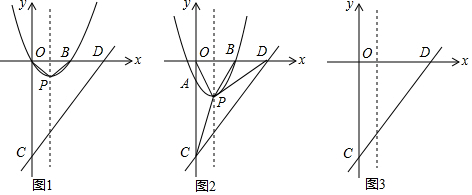
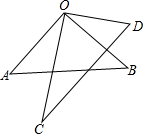 如图,∠AOB=∠COD=90°,
如图,∠AOB=∠COD=90°,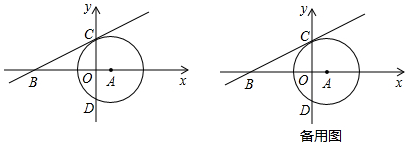
 如图,等腰三角形ABC中,AB=AC=5cm,BC=6cm,动点P从点A出发,沿路线A-B-C匀速运动,速度为1cm/s,运动到C点停止,设运动时间为t(s),△APC的面积为y(cm2).
如图,等腰三角形ABC中,AB=AC=5cm,BC=6cm,动点P从点A出发,沿路线A-B-C匀速运动,速度为1cm/s,运动到C点停止,设运动时间为t(s),△APC的面积为y(cm2).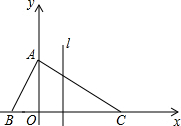 如图,△ABC的三个顶点坐标分别为(0,2),(-1,0)和(3,0),动点P从原点O出发(点P不与原点O重合),沿x轴的正方向以每秒1个单位长度的速度匀速运动,过点P作直线l⊥x轴,设点P的运动时间为t(秒).
如图,△ABC的三个顶点坐标分别为(0,2),(-1,0)和(3,0),动点P从原点O出发(点P不与原点O重合),沿x轴的正方向以每秒1个单位长度的速度匀速运动,过点P作直线l⊥x轴,设点P的运动时间为t(秒). 如图,△ABC中,AC=BC=10cm,AB=12cm,点D是AB的中点,连结CD,动点P从点A出发,沿A→C→B的路径运动,到达点B时运动停止,速度为每秒2cm,设运动时间为t秒.
如图,△ABC中,AC=BC=10cm,AB=12cm,点D是AB的中点,连结CD,动点P从点A出发,沿A→C→B的路径运动,到达点B时运动停止,速度为每秒2cm,设运动时间为t秒.