题目内容
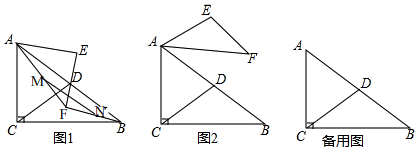
3．
如图，⊙O的直径CD=12cm，AB是⊙O的弦，AB⊥CD，垂足为E，OE：OC=1：3，则AB的长为（ ）| A． | 2$\sqrt{2}$cm | B． | 4$\sqrt{2}$cm | C． | 6$\sqrt{2}$cm | D． | 8$\sqrt{2}$cm |
分析 先求出OE再利用勾股定理即可的得出AE，最后用垂径定理即可得出AB．
解答 解：如图，
连接OA，
∵⊙O的直径CD=12cm，
∴OD=OA=OC=6，
∵OE：OC=1：3，
∴OE=2，
∵AB⊥CD，
∴AB=2AE，∠OEA=90°，
在Rt△OAE中，AE=$\sqrt{O{A}^{2}-O{E}^{2}}$=$\sqrt{36-4}$=4$\sqrt{2}$，
∴AB=2AE=8$\sqrt{2}$cm．
故选D．
点评 本题考查了垂径定理、勾股定理．解此类题一般要把半径、弦心距、弦的一半构建在一个直角三角形里，运用勾股定理求解．
练习册系列答案
相关题目
已知：如图，AB=CD，AE⊥BC，DF⊥BC，CE=BF．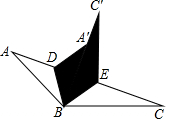
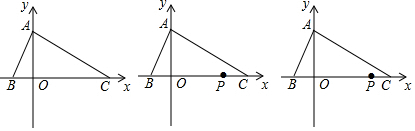
如图所示，将一张三角形纸片分别沿着BD，BE对折，使点C落在点C′，点A落在点A′，点B，A′，C′在同一条直线上，若∠ABC=130°，则∠DBE=65度．
如图，抛物线y=ax2+bx与x轴交于点A（4，0），点B（1，3）在抛物线上，点C、B关于抛物线的对称轴对称，过点B作直线BH⊥x轴，交x轴于点H．
如图，四边形ABCD中，AD=CD，AB=CB．我们把这种两组邻边分别相等的凸四边形叫做筝形．AC，BD叫作筝形的对角线．请你通过观察、测量、折纸等方法进行探究，并回答以下问题：
如图，在△ABC中，∠C=90°，sinB=$\frac{3}{5}$，AB=15，求△ABC的周长和tanA的值．
