题目内容
17. 如图,△ABC中,AC=BC=10cm,AB=12cm,点D是AB的中点,连结CD,动点P从点A出发,沿A→C→B的路径运动,到达点B时运动停止,速度为每秒2cm,设运动时间为t秒.
如图,△ABC中,AC=BC=10cm,AB=12cm,点D是AB的中点,连结CD,动点P从点A出发,沿A→C→B的路径运动,到达点B时运动停止,速度为每秒2cm,设运动时间为t秒.(1)求CD的长;
(2)当t为何值时,△ADP是直角三角形?
(3)直接写出:当t为何值时,△ADP是等腰三角形?
分析 (1)根据AC=BC=10cm,AB=12cm,点D是AB的中点,运用等腰三角形的性质,求得AD的长,再根据勾股定理求得CD即可;
(2)分两种情况进行讨论:当DP⊥AC时,△ADP是直角三角形,当PD⊥AD时,△ADP是直角三角形,分别根据相似三角形的性质进行求解即可;
(3)分三种情况进行讨论:当PA=PD时,当AP=AD时,当AD=PD时,分别作辅助线构造相似三角形,运用相似三角形的对应边成比例,求得t的值即可.
解答 解:(1)如图所示,AC=BC=10cm,AB=12cm,点D是AB的中点,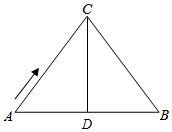
∴CD⊥AB,AD=DB=$\frac{1}{2}$AB=6cm,
∴Rt△ACD中,CD=$\sqrt{A{C}^{2}-A{D}^{2}}$=8cm;
(2)分两种情况:
①如图所示,当DP⊥AC时,△ADP是直角三角形,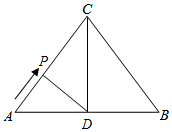
∵∠A=∠A,∠APD=∠ADC=90°,
∴△APD∽△ADC,
∴$\frac{AP}{AD}$=$\frac{AD}{AC}$,即$\frac{2t}{6}$=$\frac{6}{10}$,
解得t=1.8,
②如图所示,当PD⊥AD时,△ADP是直角三角形,
此时点P与点C重合,AP=AC=10,
∴t=$\frac{10}{2}$=5,
综上所述,当t=1.8或5秒时,△ADP是直角三角形;
(3)分三种情况:
①如图所示,当PA=PD时,过点P作PE⊥AD于E,则AE=$\frac{1}{2}$AD=3,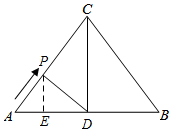
∵PE∥CD,
∴△APE∽△ACD,
∴$\frac{AP}{AC}$=$\frac{AE}{AD}$,即$\frac{2t}{10}$=$\frac{3}{6}$,
解得t=$\frac{5}{2}$;
②如图所示,当AP=AD时,2t=6,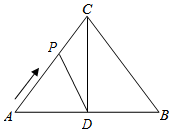
∴t=$\frac{6}{2}$=3;
③如图所示,当AD=PD时,过点D作DF⊥AP于F,则AF=$\frac{1}{2}$AP=t,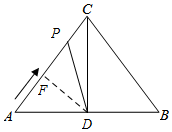
∵∠A=∠A,∠AFD=∠ADC=90°,
∴△AFD∽△ADC,
∴$\frac{AF}{AD}$=$\frac{AD}{AC}$,即$\frac{t}{6}$=$\frac{6}{10}$,
解得t=3.6,
综上所述,当t=2.5或3或3.6秒时,△ADP是等腰三角形.
点评 本题属于三角形综合题,主要考查了相似三角形的判定与性质,等腰三角形的性质以及勾股定理的应用,解决问题的关键是作辅助线构造相似三角形,根据相似三角形的对应边成比例列出比例式进行计算.解题时注意方程思想和分类思想的运用.


 如图,在△ABC中,∠C=90°,sinB=$\frac{3}{5}$,AB=15,求△ABC的周长和tanA的值.
如图,在△ABC中,∠C=90°,sinB=$\frac{3}{5}$,AB=15,求△ABC的周长和tanA的值. 如图,在正方形网格中,点O、A、B、C、D均是格点.若OE平分∠BOC,则∠DOE的度数为22.5°.
如图,在正方形网格中,点O、A、B、C、D均是格点.若OE平分∠BOC,则∠DOE的度数为22.5°.
 如图,在△ABC中,∠BAC=120°,若DE,FG分别垂直平分AB和AC,则∠EAF=60°.
如图,在△ABC中,∠BAC=120°,若DE,FG分别垂直平分AB和AC,则∠EAF=60°.