题目内容
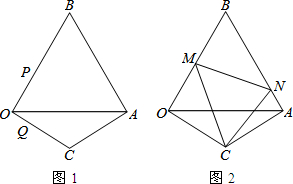
12．
如图，以AC为斜边在异侧作Rt△ABC和Rt△ADC，∠ABC=∠ADC=90°，∠BCD=45°，BD=4，则AC的长度为（ ）| A． | 8 | B． | 4$\sqrt{2}$ | C． | 6 | D． | $\sqrt{2}$ |
分析 取AC的中点O，连接OD、OB，根据题意得到A、B、C、D四点共圆，根据圆周角定理和等腰直角三角形的性质解答即可．
解答 解：取AC的中点O，连接OD、OB，
由Rt△ABC和Rt△ADC可知，A、B、C、D四点共圆，
AC为圆的直径，
∵∠BCD=45°，
∴∠BOD=90°，又BD=4，
∴OD=OB=2$\sqrt{2}$，
∴AC=4$\sqrt{2}$，
故选：B．
点评 本题考查的是圆周角定理、等腰直角三角形的性质，掌握90°的圆周角所对的弦是直径是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
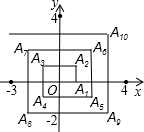如图，已知A1（1，0），A2（1，1），A3（-1，1），A4（-1，-1），A5（2，-1），…则点A2013的坐标为（504，-503）．
一个直棱柱的三视图如图所示（单位：mm），请描述这个直棱柱的形状，并画出它的表面展开图，求出它的表面积（结果保留3个有效数字）．
如图，∠D=30°，∠O=50°，∠C=35°，则∠AEC等于65°．
