题目内容
1.已知a+b=2,b≤2,y-a2-2a+2=0.则y的取值范围是y≥-2.分析 根据a+b=2、b≤2求出a的取值范围,由y-a2-2a+2=0得y=a2+2a-2=(a+1)2-3,结合自变量a的取值范围可知y的范围.
解答 解:由a+b=2,得:b=2-a,
∵b≤2,得:2-a≤2,
解得:a≥0,
∵y-a2-2a+2=0,
∴y=a2+2a-2=(a+1)2-3,
∵当a>-1时,y随a的增大而增大,
∴当a≥0时,y≥-2,
故答案为:y≥-2.
点评 本题主要考查二次函数的最值,根据已知方程得到二次函数并配方成顶点式是前提,结合自变量取值范围依据函数性质求得函数值的范围是关键.

练习册系列答案
相关题目
12. 如图,以AC为斜边在异侧作Rt△ABC和Rt△ADC,∠ABC=∠ADC=90°,∠BCD=45°,BD=4,则AC的长度为( )
如图,以AC为斜边在异侧作Rt△ABC和Rt△ADC,∠ABC=∠ADC=90°,∠BCD=45°,BD=4,则AC的长度为( )
 如图,以AC为斜边在异侧作Rt△ABC和Rt△ADC,∠ABC=∠ADC=90°,∠BCD=45°,BD=4,则AC的长度为( )
如图,以AC为斜边在异侧作Rt△ABC和Rt△ADC,∠ABC=∠ADC=90°,∠BCD=45°,BD=4,则AC的长度为( )| A. | 8 | B. | 4$\sqrt{2}$ | C. | 6 | D. | $\sqrt{2}$ |
16.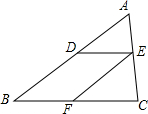 如图,在△ABC中,DE∥BC,若AD=1,BD=2,则$\frac{DE}{BC}$的值为( )
如图,在△ABC中,DE∥BC,若AD=1,BD=2,则$\frac{DE}{BC}$的值为( )
 如图,在△ABC中,DE∥BC,若AD=1,BD=2,则$\frac{DE}{BC}$的值为( )
如图,在△ABC中,DE∥BC,若AD=1,BD=2,则$\frac{DE}{BC}$的值为( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{2}{3}$ |
10.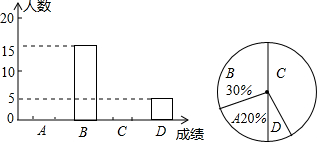 蓝天实验学校九年级一模考试后,戴主任为了解学生的学习情况,随机抽取50名学生的数学成绩(均为整数)进行统计分析,得出相关统计表和统计图如下:
蓝天实验学校九年级一模考试后,戴主任为了解学生的学习情况,随机抽取50名学生的数学成绩(均为整数)进行统计分析,得出相关统计表和统计图如下:
请根据以上所提供的信息回答下列问题:
(1)统计表中的m=10,n=20,并补全条形统计图;
(2)若该校九年级有580名学生,请据此估计该校九年级一模考试数学成绩在B等级以上(含B等级)的学生有多少名.
 蓝天实验学校九年级一模考试后,戴主任为了解学生的学习情况,随机抽取50名学生的数学成绩(均为整数)进行统计分析,得出相关统计表和统计图如下:
蓝天实验学校九年级一模考试后,戴主任为了解学生的学习情况,随机抽取50名学生的数学成绩(均为整数)进行统计分析,得出相关统计表和统计图如下:请根据以上所提供的信息回答下列问题:
| 成绩/分 | 111~120 | 101~110 | 91~100 | 90以下 |
| 成绩等级 | A | B | C | D |
| 人数 | m | 15 | n | 5 |
(2)若该校九年级有580名学生,请据此估计该校九年级一模考试数学成绩在B等级以上(含B等级)的学生有多少名.
 如图所示,AB∥CD,AD∥BC,AD=BC吗?AB=CD吗?为什么?
如图所示,AB∥CD,AD∥BC,AD=BC吗?AB=CD吗?为什么? 如图,直线L1,L2交于一点P,若y1≥y2,则x的取值范围是x≤3.
如图,直线L1,L2交于一点P,若y1≥y2,则x的取值范围是x≤3.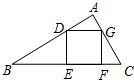 如图,△ABC中∠BAC=90°,正方形DEFG内接于△ABC,且△BDE、△CFG的面积分别为4、1,则△ADG的面积是$\frac{4}{5}$.
如图,△ABC中∠BAC=90°,正方形DEFG内接于△ABC,且△BDE、△CFG的面积分别为4、1,则△ADG的面积是$\frac{4}{5}$.