题目内容
5.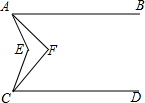 如图,已知AB∥CD,∠EAF=$\frac{1}{4}$∠EAB,∠ECF=$\frac{1}{4}$∠ECD,求证:∠AFC=$\frac{3}{4}$∠AEC.
如图,已知AB∥CD,∠EAF=$\frac{1}{4}$∠EAB,∠ECF=$\frac{1}{4}$∠ECD,求证:∠AFC=$\frac{3}{4}$∠AEC.
分析 连接AC,设∠EAF=x°,∠ECF=y°,∠EAB=4x°,∠ECD=4y°,根据平行线性质得出∠BAC+∠ACD=180°,求出∠CAE+∠ACE=180°-(4x°+4y°),求出∠AEC=4(x°+y°),∠AFC═3(x°+y°),即可得出答案.
解答 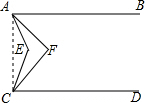 证明:连接AC,设∠EAF=x°,∠ECF=y°,∠EAB=4x°,∠ECD=4y°,
证明:连接AC,设∠EAF=x°,∠ECF=y°,∠EAB=4x°,∠ECD=4y°,
∵AB∥CD,
∴∠BAC+∠ACD=180°,
∴∠CAE+4x°+∠ACE+4y°=180°,
∴∠CAE+∠ACE=180°-(4x°+4y°),∠FAC+∠FCA=180°-(3x°+3y°)
∴∠AEC=180°-(∠CAE+∠ACE)
=180°-[180°-(4x°+4y°)]
=4x°+4y°
=4(x°+y°),
∠AFC=180°-(∠FAC+∠FCA)
=180°-[180°-(3x°+3y°)]
=3x°+3y°
=3(x°+y°),
∴∠AFC=$\frac{3}{4}$∠AEC.
点评 本题考查了平行线性质和三角形内角和定理的应用,注意:两直线平行,同旁内角互补.

练习册系列答案
相关题目
15.△ABC是一个任意三角形,用直尺和圆规作出∠A、∠B的平分线,如果两条平分线交于点O,那么下列选项中不正确的是( )
| A. | 点O一定在△ABC的内部 | B. | ∠C的平分线一定经过点O | ||
| C. | 点O到△ABC的三边距离一定相等 | D. | 点O到△ABC三顶点的距离一定相等 |
 已知一次函数y=kx+b的图象与直线y=-$\sqrt{3}$x平行且经过点(2,-$\sqrt{3}$),与x轴、y轴分别交于A,B两点.
已知一次函数y=kx+b的图象与直线y=-$\sqrt{3}$x平行且经过点(2,-$\sqrt{3}$),与x轴、y轴分别交于A,B两点.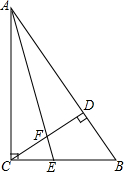 已知,如图,在△ABC中,∠ACB=90°,AE是角平分线,CD是高,AE、CD相交于点F,求证:∠CEF=∠CFE.
已知,如图,在△ABC中,∠ACB=90°,AE是角平分线,CD是高,AE、CD相交于点F,求证:∠CEF=∠CFE.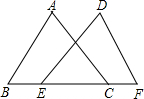 已知,如图,AB=DF,BE=FC,∠B=∠F,求证:△ABC≌△DFE.
已知,如图,AB=DF,BE=FC,∠B=∠F,求证:△ABC≌△DFE. 已知,如图,△OBC中是直角三角形,OB与x轴正半轴重合,∠OBC=90°,且OB=1,BC=$\sqrt{3}$,将△OBC绕原点O逆时针旋转60°再将其各边扩大为原来的2倍,使OB1=OC,得到△OB1C1,将△OB1C1绕原点O逆时针旋转60°再将其各边扩大为原来的2倍,使OB2=OC1,得到△OB2C2,…,如此继续下去,得到△OB2015C2015,则点C2015的坐标是(22016,0).
已知,如图,△OBC中是直角三角形,OB与x轴正半轴重合,∠OBC=90°,且OB=1,BC=$\sqrt{3}$,将△OBC绕原点O逆时针旋转60°再将其各边扩大为原来的2倍,使OB1=OC,得到△OB1C1,将△OB1C1绕原点O逆时针旋转60°再将其各边扩大为原来的2倍,使OB2=OC1,得到△OB2C2,…,如此继续下去,得到△OB2015C2015,则点C2015的坐标是(22016,0). 如图,在平行四边形ABCD中,点E为边AD的中点,连接AC,BE交于点O,则S△AOE:S△COB=1:4.
如图,在平行四边形ABCD中,点E为边AD的中点,连接AC,BE交于点O,则S△AOE:S△COB=1:4.