题目内容
17. 已知,如图,△OBC中是直角三角形,OB与x轴正半轴重合,∠OBC=90°,且OB=1,BC=$\sqrt{3}$,将△OBC绕原点O逆时针旋转60°再将其各边扩大为原来的2倍,使OB1=OC,得到△OB1C1,将△OB1C1绕原点O逆时针旋转60°再将其各边扩大为原来的2倍,使OB2=OC1,得到△OB2C2,…,如此继续下去,得到△OB2015C2015,则点C2015的坐标是(22016,0).
已知,如图,△OBC中是直角三角形,OB与x轴正半轴重合,∠OBC=90°,且OB=1,BC=$\sqrt{3}$,将△OBC绕原点O逆时针旋转60°再将其各边扩大为原来的2倍,使OB1=OC,得到△OB1C1,将△OB1C1绕原点O逆时针旋转60°再将其各边扩大为原来的2倍,使OB2=OC1,得到△OB2C2,…,如此继续下去,得到△OB2015C2015,则点C2015的坐标是(22016,0).
分析 根据直角三角形得出∠BOC=60°,然后求出OC1、OC2、OC3、…、OCn的长度,再根据周角等于360°,每6个为一个循环组,求出点C2015是第几个循环组的第几个点,再根据变化规律写出点的坐标即可.
解答 解:∵∠OBC=90°,OB=1,BC=$\sqrt{3}$,
∵将△OBC绕原点O逆时针旋转60°再将其各边扩大为原来的2倍,使OB1=OC,
∴OC1=2OC=2×2=4=22,
OC2=2OC1=2×4=8=23,
OC3=2OC2=2×8=16=24,
…,
OCn=2n+1,
∴OC2015=22016,
∵2015÷6=335…5,
∴点C2015与点C5在同一射线上,在x轴正半轴,坐标为(22016,0).
故答案为:(22016,0).
点评 本题考查了坐标与图形的变化-旋转,根据周角等于360°,每6个为一个循环组,求出点C2015是第几个循环组的第几个点是解题的关键.

练习册系列答案
相关题目
7.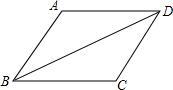 如图,在菱形ABCD中,AB=6,∠ABD=30°,则菱形ABCD的面积是( )
如图,在菱形ABCD中,AB=6,∠ABD=30°,则菱形ABCD的面积是( )
 如图,在菱形ABCD中,AB=6,∠ABD=30°,则菱形ABCD的面积是( )
如图,在菱形ABCD中,AB=6,∠ABD=30°,则菱形ABCD的面积是( )| A. | 18 | B. | 18$\sqrt{3}$ | C. | 36 | D. | 36$\sqrt{3}$ |
 已知函数y=$\frac{6}{x}$-1与函数y=kx交于点A(2,b)、B(-3,m)两点(点A在第一象限),
已知函数y=$\frac{6}{x}$-1与函数y=kx交于点A(2,b)、B(-3,m)两点(点A在第一象限),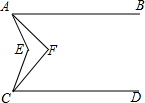 如图,已知AB∥CD,∠EAF=$\frac{1}{4}$∠EAB,∠ECF=$\frac{1}{4}$∠ECD,求证:∠AFC=$\frac{3}{4}$∠AEC.
如图,已知AB∥CD,∠EAF=$\frac{1}{4}$∠EAB,∠ECF=$\frac{1}{4}$∠ECD,求证:∠AFC=$\frac{3}{4}$∠AEC.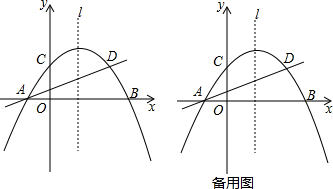
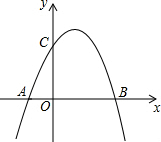 如图,二次函数y=ax2+bx+c的图象交x轴于A(-1,0),B(2,0),交y轴于C(0,2),作直线BC.
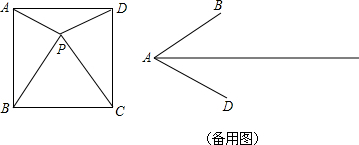
如图,二次函数y=ax2+bx+c的图象交x轴于A(-1,0),B(2,0),交y轴于C(0,2),作直线BC.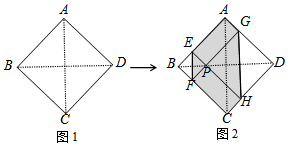 如图1,正方形纸片ABCD的边长为2,翻折∠B、∠D,使两个直角的顶点重合于对角线BD上一点P、EF、GH分别是折痕(如图2).设AE=x(0<x<2),给出下列判断:
如图1,正方形纸片ABCD的边长为2,翻折∠B、∠D,使两个直角的顶点重合于对角线BD上一点P、EF、GH分别是折痕(如图2).设AE=x(0<x<2),给出下列判断: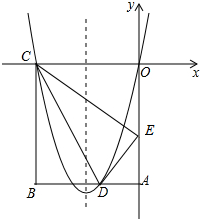 如图,在矩形OABC中,OA=5,AB=4,点D为边AB上一点,将△BCD沿直线CD折叠,使点B恰好落在边OA上的点E处,分别以OC,OA所在的直线为x轴,y轴建立平面直角坐标系.
如图,在矩形OABC中,OA=5,AB=4,点D为边AB上一点,将△BCD沿直线CD折叠,使点B恰好落在边OA上的点E处,分别以OC,OA所在的直线为x轴,y轴建立平面直角坐标系.