题目内容
4. 已知:如图,P是线段AB上的一点,分别以线段AP,PB为一边在AB的同侧作等边三角形APE和等边三角形PBF,连接EF,点G,M,N,H分别是四边形ABFE的边AB,BF,FE,EA的中点,连接HG,GM,MN和NH.求证:四边形GMNH为菱形.
已知:如图,P是线段AB上的一点,分别以线段AP,PB为一边在AB的同侧作等边三角形APE和等边三角形PBF,连接EF,点G,M,N,H分别是四边形ABFE的边AB,BF,FE,EA的中点,连接HG,GM,MN和NH.求证:四边形GMNH为菱形.
分析 欲证明四边形GMNH为菱形,只要证明HN=HG=GM=MN,由题意HN=GM=$\frac{1}{2}AF$,HG=MN=$\frac{1}{2}EB$,所以只要证明AF=EB,利用△APF≌△EPB即可证明.
解答 证明: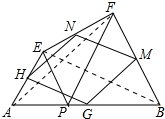 ∵△APE和△PBF都是等边三角形,
∵△APE和△PBF都是等边三角形,
∴AP=PE,PF=PB,∠APE=∠FPB=60°,
∴∠APF=∠EPB,
在△APF和△EPB中,
$\left\{\begin{array}{l}{AP=EP}\\{∠APF=∠EPB}\\{PF=PB}\end{array}\right.$,
∴△APF≌△EPB,
∴AF=EB,
∵EH=HA,EN=NF,
∴HN=$\frac{1}{2}AF$,同理GM=$\frac{1}{2}AF$,HG=MN=$\frac{1}{2}EB$,
∴HN=HG=GM=MN,
∴四边形MNHG是菱形.
点评 本题考查菱形的判定、三角形中位线的性质、全等三角形的判定和性质,解题的关键是利用全等三角形证明线段AF=EB,声音中考常考题型.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.关于x的方程3x2-2x+1=0的根的情况是( )
| A. | 有两个相等的实数根 | B. | 有两个不相等的实数根 | ||
| C. | 没有实数根 | D. | 不能确定 |
 如图,OC⊥AB于O,OD⊥OE于O,图中相等的角5对;互余的角有4对;互补的角有7对.
如图,OC⊥AB于O,OD⊥OE于O,图中相等的角5对;互余的角有4对;互补的角有7对.