题目内容
6．
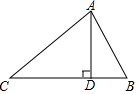△ABC中，AC=15，AB=13，BC=14，则BC边上的高AD=12．
分析 AD为高，那么题中有两个直角三角形．AD在这两个直角三角形中，设BD为未知数，可利用勾股定理都表示出AD长．求得BD长，再根据勾股定理求得AD长．
解答 解：设BD=x，则CD=14-x，
在Rt△ABD中，AD2+x2=132，
在Rt△ADC中，AD2=152-（14-x）2，
则有132-x2=152-（14-x）2，
132-x2=152-196+28x-x2，
解得x=5，
在Rt△ABD中，AD=$\sqrt{1{3}^{2}-{5}^{2}}$=12．
故答案为：12．
点评 本题考查了勾股定理，解决本题的关键在于利用两个直角三角形的公共边找到突破点．主要利用了勾股定理进行解答．
练习册系列答案
相关题目
1．若代数式$\frac{\sqrt{3x-2}}{|x|-3}$有意义，则x的取值范围是（ ）
| A． | x＞$\frac{2}{3}$且x≠3 | B． | x≥$\frac{2}{3}$ | C． | x≥$\frac{2}{3}$且x≠3 | D． | x≤$\frac{2}{3}$且x≠-3 |
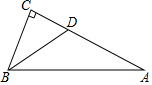如图，在△ABC中，∠C=90°，BD平分∠ABC，若BD=5，BC=4，则点D到边AB的距离为3．
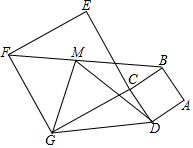如图，正方形ABCD和正方形CEFG的面积分别为4平方厘米和36平方厘米，∠DCG=90°，M是BF的中点，则三角形DMG的面积为5平方厘米．