题目内容
1．
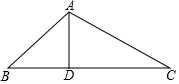如图，在△ABC中，AD⊥BC，∠B=45°，∠C=30°，AD=1，求△ABC的周长．
分析 先根据题意得出AAD=BD，再由勾股定理得出AB的长，在Rt△ADC中，根据直角三角形的性质得出AC及CD的长，进而可得出结论．
解答 解：∵AD⊥BC，
∴∠ADB=∠ADC=90°．
在Rt△ADB中，
∵∠B+∠BAD=90°，∠B=45°，
∴∠B=∠BAD=45°，
∴AD=BD=1，AB=$\sqrt{2}$．
在Rt△ADC中，
∵∠C=30°，
∴AC=2AD=2，
∴CD=$\sqrt{3}$，BC=BD+CD=1+$\sqrt{3}$，
∴AB+AC+BC=$\sqrt{2}$+$\sqrt{3}$+3．
点评 本题考查的是勾股定理，熟知在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键．
练习册系列答案
相关题目
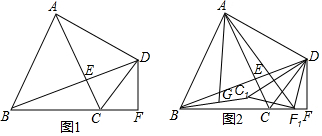
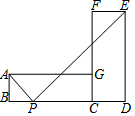如图，将矩形ABCG（AB＜BC）绕点C顺时针旋转90°后得到矩形CFED，点P是线段BD上的一个动点，连接AP、PE，则使∠APE为直角的点P的个数是（ ）
9．已知点P（x，y），且（x+1）2+$\sqrt{y-2}$=0，则点P的坐标为（ ）
| A． | （-1，0） | B． | （-1，2） | C． | （0，2） | D． | （1，-2） |
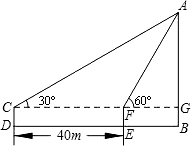如图，在一次数学课外实践活动中，要求测教学楼的高度AB．小刚在D处用高1.5米的测角仪CD，测得教学楼顶端A的仰角为30°，然后向教学楼前进40米到达E，又测得教学楼顶端A的仰角为60°，求这幢教学楼的高度AB（结果精确到0.1米，$\sqrt{3}$≈1.732）．
如图，在所给的平面直角坐标系中描出下列各点：①点A在x轴上方，y轴左侧，距离x轴4个单位长度，距离y轴2个单位长度；②点B在x轴下方，y轴右侧，距离x、y轴都是3个单位长度；③点C在y轴上，位于原点下方，距离原点2个单位长度；④点D在x轴上，位于原点右侧，距离原点4个单位长度．