题目内容
 已知二次函数y=x2-4x+3.
已知二次函数y=x2-4x+3.(1)该函数图象的顶点坐标为
(2)在右边的平面直角坐标系轴画出该函数图象;
(3)在这个函数图象上有两点A(x1,y1),B(x2,y2),且x1<x2<1,则y1
(4)如何将该图象沿x轴方向平移,能使该函数的图象经过原点?(直接写出平移方案)
考点:二次函数的性质,二次函数的图象,二次函数图象上点的坐标特征,二次函数图象与几何变换
专题:
分析:(1)将二次函数配方成顶点式后即可确定顶点坐标及对称轴;
(2)确定函数的图象与坐标轴的交点坐标后结合对称轴及顶点坐标即可画出二次函数的图象;
(3)结合函数的图象的增减性直接回答即可;
(4)利用(1)的二次函数的顶点式解析式,就可以解答函数图象的平移问题.
(2)确定函数的图象与坐标轴的交点坐标后结合对称轴及顶点坐标即可画出二次函数的图象;
(3)结合函数的图象的增减性直接回答即可;
(4)利用(1)的二次函数的顶点式解析式,就可以解答函数图象的平移问题.
解答:解:(1)y=x2-4x+3=(x-2)2-1,
所以顶点坐标为(2,-1),对称轴为直线x=2;
(2)令y=x2-4x+3=0,解得x=1或x=3,
所以图象与x轴的交点为(1,0)和(3,0),
令x=0,得:y=3,
所以图象与y轴的交点坐标为(0,3),
所以图象为:

(3)∵对称轴为x=2,函数图象的两点为A(x1,y1),B(x2,y2),且x1<x2<1,
∴y1>y2
(4)观察图象知:函数的图象向左平移1个单位或向下平移3个单位就可以经过原点;
所以顶点坐标为(2,-1),对称轴为直线x=2;
(2)令y=x2-4x+3=0,解得x=1或x=3,
所以图象与x轴的交点为(1,0)和(3,0),
令x=0,得:y=3,
所以图象与y轴的交点坐标为(0,3),
所以图象为:

(3)∵对称轴为x=2,函数图象的两点为A(x1,y1),B(x2,y2),且x1<x2<1,
∴y1>y2
(4)观察图象知:函数的图象向左平移1个单位或向下平移3个单位就可以经过原点;
点评:主要考查的是函数图象的平移及二次函数的性质,用平移规律“左加右减,上加下减”直接代入函数解析式,求得平移后的函数解析式.

练习册系列答案
相关题目
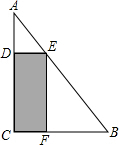 一块三角形废料如图所示,∠C=90°,cosB=
一块三角形废料如图所示,∠C=90°,cosB=| 3 |
| 5 |
A、S=-
| ||
B、S=-
| ||
C、S=-
| ||
D、S=-
|
 如图,点A(a,2)在反比例函数
如图,点A(a,2)在反比例函数 如图,点A、点B在双曲线y1=
如图,点A、点B在双曲线y1= 小王开车从甲地到相距320千米的乙地,如果油箱剩余油量y(升)与行驶里程x(千米)满足一次函数关系,其图象如图所示,则y与x的函数解析式为
小王开车从甲地到相距320千米的乙地,如果油箱剩余油量y(升)与行驶里程x(千米)满足一次函数关系,其图象如图所示,则y与x的函数解析式为