Question

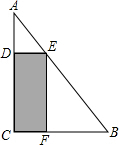一块三角形废料如图所示，∠C=90°，cosB=

3

5

，AB=2.5米，用这块废料剪出一个长方形CDEF，其中，点D、E、F分别在AC、AB、BC上．若DE为x米，长方形CDEF的面积为S平方米，则S与x之间的函数关系式为（　　）

• A、S=-

  3

  4

  x²+2x
• B、S=-

  4

  3

  x²+2x
• C、S=-

  3

  5

  x²+2x
• D、S=-

  5

  3

  x²+2x

Answer 1

考点：相似三角形的应用,根据实际问题列二次函数关系式

专题：

分析：先根据∠C=90°，cosB=

3

5

，AB=2.5米求出BC的长，再根据勾股定理得出AC的长，由四边形CDEF是长方形可得出EF∥AC，故可得出△BEF∽△BAC，根据相似三角形的对应边成比例可用x表示出EF的长，由长方形的面积公式即可得出结论．

解答：解：∵∠C=90°，cosB=

3

5

，AB=2.5米，
∴

BC

AB

=

3

5

，即

BC

2.5

=

3

5

，解得BC=1.5，
∵△ABC是直角三角形，
∴AC=

AB2-BC2

=

2.52-1.52

=2（米），
∵四边形CDEF是长方形，
∴EF∥AC，
∴△BEF∽△BAC，
∴

EF

AC

=

BF

BC

，即

EF

2

=

1.5-x

1.5

，解得EF=2-

4

3

x，
∵长方形CDEF的面积为S平方米，
∴S=DE•EF=x（2-

4

3

x）=-

4

3

x²+2x．
故选B．

点评：本题考查的是相似三角形的应用，熟知相似三角形的对应边成比例是解答此题的关键．