题目内容
18.计算:(1)(-1)2008+($\frac{1}{{\sqrt{3}+1}}$)0+(-$\frac{1}{2}$)-1
(2)-22+($\frac{1}{2}$)-2-|π-3|0+$\root{3}{-8}$
(3)$\frac{a^2}{a-1}$+a+1
(4)$\frac{a-b}{a+b}$÷(b-a)•$\frac{1}{a-b}$.
分析 (1)零次幂都等于1,(-$\frac{1}{2}$)-1=(-2)1=-2;
(2)注意-22=-4,$\root{3}{-8}$=-2;
(3)通分,把a+1看成是$\frac{a+1}{1}$,公分母是a-1;
(4)按从左到右的顺序计算,把除法变成乘法.
解答 解:(1)(-1)2008+($\frac{1}{{\sqrt{3}+1}}$)0+(-$\frac{1}{2}$)-1,
=1+1+(-2),
=0;
(2)-22+($\frac{1}{2}$)-2-|π-3|0+$\root{3}{-8}$,
=-4+4-1-2,
=-3;
(3)$\frac{a^2}{a-1}$+a+1,
=$\frac{{a}^{2}}{a-1}$+$\frac{{a}^{2}-1}{a-1}$,
=$\frac{{a}^{2}+{a}^{2}-1}{a-1}$,
=$\frac{2{a}^{2}-1}{a-1}$;
(4)$\frac{a-b}{a+b}$÷(b-a)•$\frac{1}{a-b}$,
=$\frac{a-b}{a+b}$×$\frac{1}{b-a}$×$\frac{1}{a-b}$,
=$\frac{1}{(a+b)(b-a)}$,
=$\frac{1}{{b}^{2}-{a}^{2}}$.
点评 本题考查了分式和实数的运算,熟练掌握以下几个公式和性质是关键:①零指数幂:a0=1(a≠0);②负整数指数幂:a-p=$\frac{1}{{a}^{p}}$(a≠0,p为正整数);③负整数指数幂:当底数是分数时,只要把分子、分母颠倒,负指数就可变为正指数;④在进行实数运算时,和有理数运算一样,要从高级到低级,即先算乘方、开方,再算乘除,最后算加减,有括号的要先算括号里面的,同级运算要按照从左到有的顺序进行.

 名校课堂系列答案
名校课堂系列答案| A. | 2x-6+x=30 | B. | x+6+2x=30 | C. | $\frac{1}{2}$x+6+x=30 | D. | $\frac{1}{2}$x+6+x=30 |
| A. | 矩形 | B. | 菱形 | C. | 正方形 | D. | 平行四边形 |
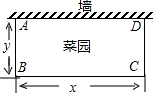 李大爷要围成一个矩形菜园,菜园的一边利用足够长的墙、用篱笆围成的另外三边总长恰好为24米,要围成的菜园是如图所示的长方形ABCD,设BC边的长为x米,AB边的长为y米.
李大爷要围成一个矩形菜园,菜园的一边利用足够长的墙、用篱笆围成的另外三边总长恰好为24米,要围成的菜园是如图所示的长方形ABCD,设BC边的长为x米,AB边的长为y米.