Question

10．已知E、F、G、H是矩形ABCD各边的中点，则四边形EFGH的形状是（　　）

• A． 矩形
• B． 菱形
• C． 正方形
• D． 平行四边形

Answer 1

分析 连接BD，根据三角形的中位线定理得到EH∥BD，EH=$\frac{1}{2}$BD，FG∥BD，FG═$\frac{1}{2}$BD，推出，EH∥FG，EH=FG，根据一组对边平行且相等的四边形是平行四边形得出四边形EFGH是平行四边形．

解答 解：如图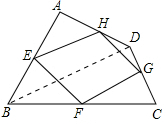，连结BD．
∵E、H分别是AB、AD中点，
∴EH∥BD，EH=$\frac{1}{2}$BD，
同理FG∥BD，FG=$\frac{1}{2}$BD，
∴EH∥FG，EH=FG，
∴四边形EFGH是平行四边形；
故选：D．

点评 本题主要考查对三角形的中位线定理，平行四边形的判定等知识点的理解和掌握，熟练掌握各定理是解决此题的关键．