题目内容
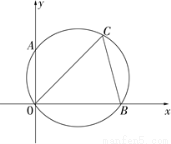
二次函数y=ax2+bx+c(a≠0)的图象如图所示,则比较下列大小:

①abc 0;②4a+2b+c 0;③2c 3b;④a+b m(am+b).
<;>;<;≥
【解析】
试题分析:①由图象可知:a<0,b>0,c>0,可得abc<0,②由对称可知,当x=2时,函数值大于0,即y=4a+2b+c>0,③当x=3时函数值小于0,y=9a+3b+c<0,且x=- =1,即a=-
=1,即a=- ,代入得9(-
,代入得9(- )+3b+c<0,得2c<3b,④当x=1时,y的值最大.此时,y=a+b+c,而当x=m时,y=am2+bm+c,所以a+b+c≥am2+bm+c,故a+b≥am2+bm,即a+b≥m(am+b).
)+3b+c<0,得2c<3b,④当x=1时,y的值最大.此时,y=a+b+c,而当x=m时,y=am2+bm+c,所以a+b+c≥am2+bm+c,故a+b≥am2+bm,即a+b≥m(am+b).
考点:二次函数图象与系数的关系.

练习册系列答案
相关题目
 C.1,1,
C.1,1, D.1,2,
D.1,2,
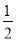 B.
B.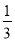 C.
C.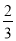 D.
D.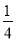
 ,所以
,所以 ,从而
,从而 (当x=
(当x= 时取等号).记函数
时取等号).记函数 ,由上述结论可知:当x=
,由上述结论可知:当x= ,则当x= 时,y1+y2取得最小值为
,则当x= 时,y1+y2取得最小值为  的最小值,并指出取得该最小值时相应的x的值.
的最小值,并指出取得该最小值时相应的x的值. ,则
,则 的值为
的值为 
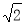 ).
).