题目内容
已知:△OBC内接于圆,圆与直角坐标系的x、y轴交于B、A两点,若∠BOC=45°,∠OBC=75°,A点坐标为(0,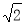 ).
).
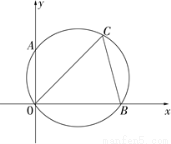
求:⑴B点的坐标;
⑵BC的长.
【解析】
(1)连接AB

∵∠BOC=45°,∠OBC=75°,
∴∠OAB=∠OCB=60°
∵A点坐标为(0, ),
),
∴AO= .
.
在Rt△AOB中,∠OBA=30°∴AB=2
∴OB2=AB2-OA2=8-2=6
∴OB=
∴B( ,0)
,0)
(2) 作BE⊥OC于E(4分).
∵∠BOE=45°,
∴OE=BE.
在Rt△BEO中,OE2+BE2=OB2,0E=BE=
在Rt△BEC中, CE2+BE2=CB2 BC=2CE
∴BC=2
【解析】
试题分析:(1)构造以AB为斜边的直角三角形,利用三角形的内角和定理可得∠C的度数,利用
同弧所对的圆周角相等可得∠OAB的度数,进而利用∠OAB的正切值可求得OB长,也就求得了点
B的坐标;(2)作出以BC为斜边的直角三角形,利用45°的余弦值可求得BE长,进而利用60°
的正弦值可求得BC长.
考点:解直角三角形,圆周角定理

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 ,若点P满足PD=1,且∠BPD=90°,请求出点A到BP的距离.
,若点P满足PD=1,且∠BPD=90°,请求出点A到BP的距离.
 中,动点
中,动点 从点
从点 出发,依次沿对角线
出发,依次沿对角线 、边
、边 、边
、边 运动至点
运动至点 停止,设点
停止,设点 的运动路程为
的运动路程为 ,
,  .则矩形
.则矩形

 的值是
的值是 B.
B. C.
C. D.
D.
 的直径,CD是⊙O的一条弦,且CD⊥AB于点E.
的直径,CD是⊙O的一条弦,且CD⊥AB于点E.
 证:∠BCO=∠D;
证:∠BCO=∠D;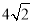 ,AE=2,求⊙O的半径.
,AE=2,求⊙O的半径.
 .
.