Question

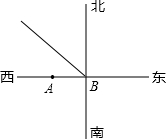在某岛A的正东方向有台风，且台风中心B距离小岛A40

2

km，台风中心正以30km/h的速度向西北方向移动，距离中心50公里以内圆形区域（包括边界）都受影响，则小岛A受到台风影响的时间为（　　）

• A、不受影响
• B、1小时
• C、2小时
• D、3小时

Answer 1

考点：垂径定理的应用,勾股定理

专题：计算题

分析：假设D与E刚好受影响，连接AD，AE，可得出AD=AE=50公里，过A作AC垂直于BE，可得出EC=CD，由BE为西北方向，得到三角形ABC为等腰直角三角形，由AB的长求出AC的长，在直角三角形ACD中，有AC与AD的长，利用勾股定理求出CD的长，进而确定出ED的长，除以台风的速度，即可求出受影响的时间．

解答：解：假设D、E为刚好受影响的点，
过A作AC⊥BE，连接AE、AD，可得出AE=AD=50公里，
∵BE为西北方向，
∴∠ABE=45°，又∠ACB=90°，AB=40

2

公里，
∴AC=BC=40公里，
在Rt△ADC中，AD=50公里，AC=40公里，
根据勾股定理得：DC=

AD2-AC2

=30公里，
∴ED=2DC=60公里，又台风速度为30公里/时，
则小岛A受到台风影响的时间为60÷30=2（小时）．
故选C．

点评：此题考查了垂径定理的应用，等腰三角形的性质，等腰直角三角形的判定与性质，以及勾股定理，熟练掌握定理是解本题的关键．