题目内容
解方程:
(1)3x2-5x=1(用配方法解)
(2)4y2-1=4(2y+1)
(1)3x2-5x=1(用配方法解)
(2)4y2-1=4(2y+1)
考点:解一元二次方程-因式分解法,解一元二次方程-配方法
专题:
分析:(1)根据配方法的一般步骤:首先把二次项的系数化为1;再根据等式两边同时加上一次项系数一半的平方配方计算即可;
(2)首先把方程整理成4y2-8y-5=0,再用公式法计算即可.
(2)首先把方程整理成4y2-8y-5=0,再用公式法计算即可.
解答:解:(1)把二次项的系数化为1,得:
x2-
x=
,
等式两边同时加上一次项系数一半的平方,得:
x2-
x+(
)2=
+(
)2,
(x-
)2=
,
两边直接开平方得:x-
=±
,
∴x=
;
(2)把方程整理得:4y2-8y-5=0,
∵a=4,b=-8,c=-5,
∴△=(-8)2-4×4×(-5)=144,
∴y=
=
,
∴y1=-
,y2=
.
x2-
| 5 |
| 3 |
| 1 |
| 3 |
等式两边同时加上一次项系数一半的平方,得:
x2-
| 5 |
| 3 |
| 5 |
| 6 |
| 1 |
| 3 |
| 5 |
| 6 |
(x-
| 5 |
| 6 |
| 37 |
| 36 |
两边直接开平方得:x-
| 5 |
| 6 |
|
∴x=
5±
| ||
| 6 |
(2)把方程整理得:4y2-8y-5=0,
∵a=4,b=-8,c=-5,
∴△=(-8)2-4×4×(-5)=144,
∴y=
8±
| ||
| 2×4 |
| 2±3 |
| 2 |
∴y1=-
| 1 |
| 2 |
| 5 |
| 2 |
点评:此题考查了配方法解一元二次方程,以及公式法解一元二次方程,解题时要注意解题步骤的准确应用.选择用配方法解一元二次方程时,最好使方程的二次项的系数为1,一次项的系数是2的倍数.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
小彬在下面的计算中只做错了一道题,他做错的题目是( )
| A、(a-1)(a+1)=a2-1 |
| B、(-2a3)2=4a6 |
| C、a3÷a2=a |
| D、(a-1)2=a2-1 |
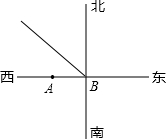 在某岛A的正东方向有台风,且台风中心B距离小岛A
在某岛A的正东方向有台风,且台风中心B距离小岛A 如图,AD∥BC,∠BAD=90°,以点B为圆心,BC长为半径画弧,与射线AD相交于点E,连接BE,过C点作CF⊥BE,垂足为F.若AB=2,BC=3,则BF的长为
如图,AD∥BC,∠BAD=90°,以点B为圆心,BC长为半径画弧,与射线AD相交于点E,连接BE,过C点作CF⊥BE,垂足为F.若AB=2,BC=3,则BF的长为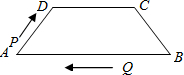 在等腰梯形ABCD中,AB∥DC,AD=BC=6cm,DC=7cm,AB=12cm,点P从点A出发,以每秒3cm的速度沿AD→DC向终点C运动,同时点Q从点B出发,以每秒2cm的速度沿BA向终点A运动.在运动期间,当四边形AQPD为平行四边形时,运动时间为( )
在等腰梯形ABCD中,AB∥DC,AD=BC=6cm,DC=7cm,AB=12cm,点P从点A出发,以每秒3cm的速度沿AD→DC向终点C运动,同时点Q从点B出发,以每秒2cm的速度沿BA向终点A运动.在运动期间,当四边形AQPD为平行四边形时,运动时间为( )