题目内容
10.已知实数m,n满足关系式$\sqrt{(n-2)^{2}(m-3)}$=-(n-2)$\sqrt{m-3}$,化简|m-3|-$\sqrt{{n}^{2}-4n+4}$.分析 由$\sqrt{(n-2)^{2}(m-3)}$=-(n-2)$\sqrt{m-3}$可知:n-2<0,m-3>0,进一步化简|m-3|-$\sqrt{{n}^{2}-4n+4}$即可.
解答 解:∵实数m,n满足关系式$\sqrt{(n-2)^{2}(m-3)}$=-(n-2)$\sqrt{m-3}$,
∴n-2<0,m-3>0,
即n<2,m>3,
∴|m-3|-$\sqrt{{n}^{2}-4n+4}$
=m-3+n-2
=m+n-5.
点评 本题主要考查二次根式的性质与化简、不等式的性质,关键在于推出m、n的取值范围.

练习册系列答案
相关题目
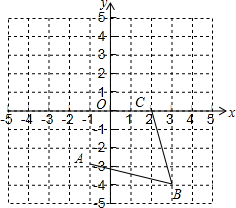 如图,在平面直角坐标系中,网格中每一个小正方形的边长为1个单位长度,
如图,在平面直角坐标系中,网格中每一个小正方形的边长为1个单位长度, 如图所示,在四边形ABCD中,∠A与∠C互补,BE平分∠ABC,DF平分∠ADC,若BE∥DF,求证:△DCF为直角三角形.
如图所示,在四边形ABCD中,∠A与∠C互补,BE平分∠ABC,DF平分∠ADC,若BE∥DF,求证:△DCF为直角三角形. 如图所示,在Rt△ABC中,∠C=90°,∠A=15°,BC=1,求△ABC的面积.
如图所示,在Rt△ABC中,∠C=90°,∠A=15°,BC=1,求△ABC的面积.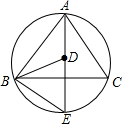 如图,AE平分∠BAC,交△ABC的外接圆于点E,D是AE上一点,且ED=EB,点D是否是△ABC的内心?为什么?
如图,AE平分∠BAC,交△ABC的外接圆于点E,D是AE上一点,且ED=EB,点D是否是△ABC的内心?为什么?