题目内容
16.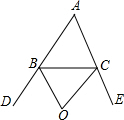 如图,BO、CO分别是△ABC的外角平分线.
如图,BO、CO分别是△ABC的外角平分线.(1)若∠A=50°,求∠BOC的度数;
(2)若∠A=α,直接写出∠BOC的度数(用α表示)
分析 (1)由三角形的一个外角等于与它不相邻的两个内角的和可证2∠1+2∠2=2∠A+∠ABC+∠ACB=∠A+180°,再根据三角形内角和定理可证2∠BOC=180°-∠A,即∠BOC=90°-$\frac{1}{2}$∠A,由此可得出结论;
(2)根据(1)的证明过程可得出结论.
解答 解:(1)∵BO、CO分别是△ABC的外角∠DBC、∠ECB的角平分线,
∴∠DBC=2∠1=∠ACB+∠A,
∠ECB=2∠2=∠ABC+∠A,
∴2∠1+2∠2=2∠A+∠ABC+∠ACB=∠A+180°,
又∵∠1+∠2+∠BOC=180°,
∴2∠BOC=180°-∠A,
∴∠BOC=90°-$\frac{1}{2}$∠A=90°-$\frac{1}{2}$×50°=90°-25°=65°;
(2)∵BO、CO分别是△ABC的外角∠DBC、∠ECB的角平分线,
∴∠DBC=2∠1=∠ACB+∠A,
∠ECB=2∠2=∠ABC+∠A,
∴2∠1+2∠2=2∠A+∠ABC+∠ACB=∠A+180°,
又∵∠1+∠2+∠BOC=180°,
∴2∠BOC=180°-∠A,
∴∠BOC=90°-$\frac{1}{2}$∠A=90°-$\frac{1}{2}$α.
点评 本题考查三角形外角的性质及三角形的内角和定理,解答的关键是沟通外角和内角的关系.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
6.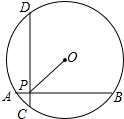 如图,在半径为10的⊙O中,AB,CD是互相垂直的两条弦,垂足为P,且AB=CD=16,则OP的长为( )
如图,在半径为10的⊙O中,AB,CD是互相垂直的两条弦,垂足为P,且AB=CD=16,则OP的长为( )
 如图,在半径为10的⊙O中,AB,CD是互相垂直的两条弦,垂足为P,且AB=CD=16,则OP的长为( )
如图,在半径为10的⊙O中,AB,CD是互相垂直的两条弦,垂足为P,且AB=CD=16,则OP的长为( )| A. | 6 | B. | 6$\sqrt{2}$ | C. | 8 | D. | 8$\sqrt{2}$ |
 如图,在△ABC中,分别画出:
如图,在△ABC中,分别画出: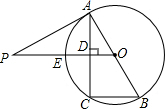 如图,已知AB为⊙O的直径,PA与⊙O相切于点A,线段OP与弦AC垂直并相交于点D,OP与弧AC相交于点E,连接BC.
如图,已知AB为⊙O的直径,PA与⊙O相切于点A,线段OP与弦AC垂直并相交于点D,OP与弧AC相交于点E,连接BC. 已知,等腰△ABC中,AB=AC,点D、E分别在边BC、AC上,且∠ADE=∠C,求证:△ABD∽△DCE.
已知,等腰△ABC中,AB=AC,点D、E分别在边BC、AC上,且∠ADE=∠C,求证:△ABD∽△DCE. 如图所示,在四边形ABCD中,∠A与∠C互补,BE平分∠ABC,DF平分∠ADC,若BE∥DF,求证:△DCF为直角三角形.
如图所示,在四边形ABCD中,∠A与∠C互补,BE平分∠ABC,DF平分∠ADC,若BE∥DF,求证:△DCF为直角三角形.
 如图所示,在Rt△ABC中,∠C=90°,∠A=15°,BC=1,求△ABC的面积.
如图所示,在Rt△ABC中,∠C=90°,∠A=15°,BC=1,求△ABC的面积.