题目内容
4.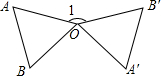 如图,将等边△OAB绕O点按逆时针方向旋转150°,得到△OA′B′(点A′,B′分别是点A,B的对应点),则∠1=150°.
如图,将等边△OAB绕O点按逆时针方向旋转150°,得到△OA′B′(点A′,B′分别是点A,B的对应点),则∠1=150°.
分析 首先根据旋转的性质得到∠AOA′=150°,然后根据∠A′OB′=60°得到∠1=360°-∠AOA′-∠A′OB′即可求解.
解答 解:∵等边△OAB绕点O按逆时针旋转了150°,得到△OA′B′,
∴∠AOA′=150°,
∵∠A′OB′=60°,
∴∠1=360°-∠AOA′-∠A′OB′=360°-150°-60°=150°,
故答案为:150.
点评 本题考查了旋转的性质:旋转前后两图形全等;对应点到旋转中心的距离相等;对应点与旋转中心的连线段的夹角等于旋转角.也考查了等边三角形的性质.

练习册系列答案
 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
14.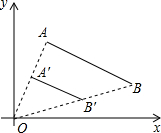 如图,线段AB的两个端点坐标分别为A(1,4),B(6,2),以原点O为位似中心,将线段AB缩小后得到线段A′B′.若AB=2A′B′,则端点B′的坐标为( )
如图,线段AB的两个端点坐标分别为A(1,4),B(6,2),以原点O为位似中心,将线段AB缩小后得到线段A′B′.若AB=2A′B′,则端点B′的坐标为( )
 如图,线段AB的两个端点坐标分别为A(1,4),B(6,2),以原点O为位似中心,将线段AB缩小后得到线段A′B′.若AB=2A′B′,则端点B′的坐标为( )
如图,线段AB的两个端点坐标分别为A(1,4),B(6,2),以原点O为位似中心,将线段AB缩小后得到线段A′B′.若AB=2A′B′,则端点B′的坐标为( )| A. | (2,2) | B. | (3,2) | C. | (2,1) | D. | (3,1) |
12.若关于x的方程$\frac{ax-1}{2-x}=\frac{3}{4}$无解,则a的值为( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | $-\frac{3}{4}$ | D. | $\frac{1}{2}$或$-\frac{3}{4}$ |
9.230 000用科学记数法表示应为( )
| A. | 0.23×105 | B. | 23×104 | C. | 2.3×105 | D. | 2.3×104 |
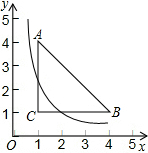 如图,已知△ABC三个顶点的坐标分别为A(1,4),B(4,1),C(1,1),若双曲线y=$\frac{k}{x}$(x>0)与△ABC有公共点,则k的取值范围是1≤k≤$\frac{25}{4}$.
如图,已知△ABC三个顶点的坐标分别为A(1,4),B(4,1),C(1,1),若双曲线y=$\frac{k}{x}$(x>0)与△ABC有公共点,则k的取值范围是1≤k≤$\frac{25}{4}$.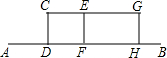 某兴趣小组开展课外活动.如图,A,B两地相距12米,小明从点A出发沿AB方向匀速前进,2秒后到达点D,此时他(CD)在某一灯光下的影长为AD,继续按原速行走2秒到达点F,此时他在同一灯光下的影子仍落在其身后,并测得这个影长为1.2米,然后他将速度提高到原来的1.5倍,再行走2秒到达点H,此时他(GH)在同一灯光下的影长为BH(点C,E,G在一条直线上).
某兴趣小组开展课外活动.如图,A,B两地相距12米,小明从点A出发沿AB方向匀速前进,2秒后到达点D,此时他(CD)在某一灯光下的影长为AD,继续按原速行走2秒到达点F,此时他在同一灯光下的影子仍落在其身后,并测得这个影长为1.2米,然后他将速度提高到原来的1.5倍,再行走2秒到达点H,此时他(GH)在同一灯光下的影长为BH(点C,E,G在一条直线上).
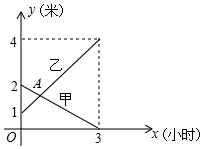 有甲、乙两个圆柱体的蓄水池,将甲池中的水以一定的速度注入乙池.甲、乙两个蓄水池中水的深度y(米)与注水时间x(时)之间的函数图象如图所示,其中,甲蓄水池中水的深度y(米)与注水时间x(时)之间的函数关系式为y=-$\frac{2}{3}$x+2.结合图象回答:
有甲、乙两个圆柱体的蓄水池,将甲池中的水以一定的速度注入乙池.甲、乙两个蓄水池中水的深度y(米)与注水时间x(时)之间的函数图象如图所示,其中,甲蓄水池中水的深度y(米)与注水时间x(时)之间的函数关系式为y=-$\frac{2}{3}$x+2.结合图象回答: