题目内容
10.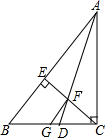 如图,在直角△ABC中,∠ACB=90°,∠BAC的平分线交BC于D,CE⊥AB于点E,交AD于点F,取BG=CD,连接FG,求证:FG∥AB.
如图,在直角△ABC中,∠ACB=90°,∠BAC的平分线交BC于D,CE⊥AB于点E,交AD于点F,取BG=CD,连接FG,求证:FG∥AB.
分析 如图,作DH⊥AB于H,易证CE∥DH,则∠1=∠2;由AD平分∠BAC,可知CD=DH,根据等角的余角相等可知∠5=∠7,所以CD=CF,所以DH=CF;由BG=CD可知BD=GC;由根据以上条件可证△BHD≌△GFC,得到∠BHD=∠GFC=∠BEC=90°,所以FG∥AB.
解答 证明:作DH⊥AB于H,
∵CE⊥AB,
∴∠CEB=∠DHB=90°,
∴CE∥DH,
∴∠1=∠2,
又∵∠ACB=90°,AD平分∠BAC,
∴DH=DC,∠3=∠4,
∵∠5=∠6=90°-∠3,
∠7=90°-∠4,
∴∠5=∠7,
∴CD=CF,
∴DH=CF,
∵BG=CD,
∴BG+GD=CD+GD,
即BD=GC,
在△BHD和△GFC中
$\left\{\begin{array}{l}{BD=GC}\\{∠1=∠2}\\{DH=CF}\end{array}\right.$,
∴△BHD≌△GFC,
∴∠BHD=∠GFC=90°,
∴∠GFC=∠BEC=90°,
∴FG∥AB.
点评 本题主要考查了全等三角形的判定与性质、角平分线性质、平行线的判定与性质等知识的综合运用,作DH⊥AB于H,证明△BHD≌△GFC是整个问题的关键.

练习册系列答案
相关题目
20.已知多项式x2+3x=3,可求得另一个多项式3x2+9x-4的值为( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
5.为丰富学生课外活动,某校积极开展社团活动,学生可根据自己的爱好选择一项,已知该校开设的体育社团有:A:篮球,B:排球C:足球;D:羽毛球,E:乒乓球.李老师对某年级同学选择体育社团情况进行调查统计,制成了两幅不完整的统计图(如图),则以下结论不正确的是( )
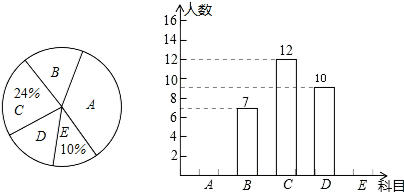

| A. | 选科目E的有5人 | |
| B. | 选科目D的扇形圆心角是72° | |
| C. | 选科目A的人数占体育社团人数的一半 | |
| D. | 选科目B的扇形圆心角比选科目D的扇形圆心角的度数少21.6° |
20.根据国家发改委实施“阶梯电价”的有关文件要求,某市结合地方实际,决定从2013年5月1日起对居民生活用电试行“阶梯电价”收费,具体收费标准见下表:
2013年5月份,该市居民甲用电200千瓦时,交电费122.5元;居民乙用电400千瓦时,交电费277.5元.
(1)求表中a,b的值;
(2)试行“阶梯电价”收费以后,该市一户居民月用电多少千瓦时,其当月的平均电价每千瓦时不超过0.62元?
| 一户居民一个月用电量的范围 | 电费价格(单位:元/千瓦时) |
| 不超过150千瓦时的部分 | a |
| 超过150千瓦时但不超过300千瓦时的部分 | b |
| 超过300千瓦时的部分 | a+0.3 |
(1)求表中a,b的值;
(2)试行“阶梯电价”收费以后,该市一户居民月用电多少千瓦时,其当月的平均电价每千瓦时不超过0.62元?
 一次综合实践活动中,小明同学拿到一只含45°角的三角板和一只含30°角的三角板,如图放置恰好有一边重合,则S△ODC:S△OAB的值为$\frac{3+\sqrt{3}}{3}$.
一次综合实践活动中,小明同学拿到一只含45°角的三角板和一只含30°角的三角板,如图放置恰好有一边重合,则S△ODC:S△OAB的值为$\frac{3+\sqrt{3}}{3}$.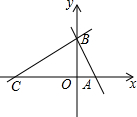 如图,平面直角坐标系中,直线y=-$\sqrt{3}x$+$\sqrt{3}$与坐标轴分别交于点A、B,且点C在x轴负半轴上,且AB:AC=1:2.
如图,平面直角坐标系中,直线y=-$\sqrt{3}x$+$\sqrt{3}$与坐标轴分别交于点A、B,且点C在x轴负半轴上,且AB:AC=1:2.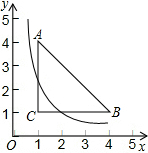 如图,已知△ABC三个顶点的坐标分别为A(1,4),B(4,1),C(1,1),若双曲线y=$\frac{k}{x}$(x>0)与△ABC有公共点,则k的取值范围是1≤k≤$\frac{25}{4}$.
如图,已知△ABC三个顶点的坐标分别为A(1,4),B(4,1),C(1,1),若双曲线y=$\frac{k}{x}$(x>0)与△ABC有公共点,则k的取值范围是1≤k≤$\frac{25}{4}$.