题目内容
16.为了解“阳光体育”活动情况,我市教育部门在某所初中2000名学生中,随机抽取了若干学生进行问卷调查(要求每位学生只能填写一种自己喜欢的活动),并将调查的结果绘制成如图的两个不完整的统计图:
根据以上信息解答下列问题:
(1)参加调查的人数共有300人,在扇形图中,表示“C”的扇形的圆心角为108度;
(2)补全条形统计图,并计算扇形统计图中的n;
(3)估计该校喜欢“B”项目的学生一共有多少人?
分析 (1)用喜欢乒乓球的人数除以其所占的百分比即可求得调查的总人数;
(2)用喜欢C项目的人数除以总人数即可求得其百分率,从而得到m的值;
(3)求出喜欢B类项目的占总数的百分比乘总人数即可.
解答 解:(1)观察统计图知喜欢乒乓球的有69人,占总人数的23%,
故调查的总人数有69÷23%=300人,
喜欢跳绳的有300-60-69-36-45=90人,
故C所表示的扇形的圆心角为$\frac{90}{300}$×360°=108°;
(2)m%=$\frac{60}{300}$×100%=20%,故m=20;
统计图如下: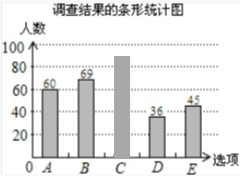
(3)喜欢B项目的有2000×23%=460人.
答:该校喜欢“B”项目的学生一共有460人.
点评 本题考查了条形统计图,解题的关键是仔细的观察两种统计图,并结合两种统计图得到解题的有关信息.

练习册系列答案
相关题目
 如图,将Rt△ABC沿斜边翻折得到△ADC,点E,F分别为DC,BC边上的点,且∠EAF=$\frac{1}{2}$∠DAB.试猜想DE,BF,EF之间有何数量关系,并证明你的猜想.
如图,将Rt△ABC沿斜边翻折得到△ADC,点E,F分别为DC,BC边上的点,且∠EAF=$\frac{1}{2}$∠DAB.试猜想DE,BF,EF之间有何数量关系,并证明你的猜想. 如图,在平面直角坐标系中,△ABC的顶点都在方格纸的格点上,如果将△ABC先向右平移4个单位长度,再向下平移1个单位长度,得到△A1B1C1,那么点A的对应点A1的坐标为(2,5).
如图,在平面直角坐标系中,△ABC的顶点都在方格纸的格点上,如果将△ABC先向右平移4个单位长度,再向下平移1个单位长度,得到△A1B1C1,那么点A的对应点A1的坐标为(2,5). 如图,△ABC的角平分线BO、CO相交于点O,∠A=120°,则∠BOC=150°.
如图,△ABC的角平分线BO、CO相交于点O,∠A=120°,则∠BOC=150°. 如图,在平面直角坐标系xOy中,抛物线y=ax2-4ax-5a(a<0)与x轴交于A、B两点(点A在点B的左侧),经过点A的直线l:y=kx+b与y轴负半轴交于点C,与抛物线的另一个交点为D,且CD=6AC.
如图,在平面直角坐标系xOy中,抛物线y=ax2-4ax-5a(a<0)与x轴交于A、B两点(点A在点B的左侧),经过点A的直线l:y=kx+b与y轴负半轴交于点C,与抛物线的另一个交点为D,且CD=6AC. 如图,EB和EC分别平分△ABC的内角,请你判断∠BEC一定是什么角,并说明理由.
如图,EB和EC分别平分△ABC的内角,请你判断∠BEC一定是什么角,并说明理由.