题目内容
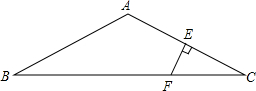
7. 如图,将Rt△ABC沿斜边翻折得到△ADC,点E,F分别为DC,BC边上的点,且∠EAF=$\frac{1}{2}$∠DAB.试猜想DE,BF,EF之间有何数量关系,并证明你的猜想.
如图,将Rt△ABC沿斜边翻折得到△ADC,点E,F分别为DC,BC边上的点,且∠EAF=$\frac{1}{2}$∠DAB.试猜想DE,BF,EF之间有何数量关系,并证明你的猜想.
分析 通过延长CF,将DE和BF放在一起,便于寻找等量关系,通过两次三角形全等证明,得出结论.
解答 猜想:DE+BF=EF.证明:延长CF,作∠4=∠1,如图:
∵将Rt△ABC沿斜边翻折得到△ADC,点E,F分别为DC,BC边上的点,且∠EAF=$\frac{1}{2}$∠DAB,
∴∠1+∠2=∠3+∠5,∠2+∠3=∠1+∠5,
∵∠4=∠1,
∴∠2+∠3=∠4+∠5,
∴∠GAF=∠FAE,
在△AGB和△AED中,$\left\{\begin{array}{l}{∠4=∠1}\\{AB=AD}\\{∠ABG=∠ADE}\end{array}\right.$,
∴△AGB≌△AED(ASA),
∴AG=AE,BG=DE,
在△AGF和△AEF中,$\left\{\begin{array}{l}{AG=AE}\\{∠GAF=∠EAF}\\{AF=AF}\end{array}\right.$,
∴△AGF≌△AEF(SAS),
∴GF=EF,
∴DE+BF=EF.
证毕.
点评 本题考查了全等三角形的判定与性质,解题的关键是作辅助角,将DE和BF放在一起,便于数量关系的猜想和证明.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
19.某学校开展“文明礼仪”演讲比赛,八(1)、八(2)班派出的5名选手的比赛成绩如图所示:

(1)填表:
(2)根据题中数据计算八(2)班成绩的方差为160,请计算八(1)班成绩的方差,判断哪个班级选手的成绩更为稳定?并说明理由.

(1)填表:
| 平均数(分) | 中位数(分) | 众数(分) | |
| 八(1)班 | 75 | 75 | 75 |
| 八(2)班 | 75 | 70 | 90 |
 如图,已知在△ABC中,AB=AC,∠BAC=120°,AC的垂直平分线EF交AC于点E,交BC于点F.试探索BF与CF的数量关系,写出你的结论并证明.
如图,已知在△ABC中,AB=AC,∠BAC=120°,AC的垂直平分线EF交AC于点E,交BC于点F.试探索BF与CF的数量关系,写出你的结论并证明.
 如图所示.求∠A+∠B+∠C+∠D+∠E+∠F的度数.
如图所示.求∠A+∠B+∠C+∠D+∠E+∠F的度数.