题目内容
19.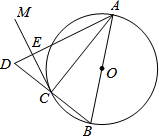 如图,AB是⊙O的直径,点C在⊙O上,过点C作⊙O的切线CM.
如图,AB是⊙O的直径,点C在⊙O上,过点C作⊙O的切线CM.(1)求证:∠ACM=∠ABC;
(2)延长BC到D,使CD=BC,连接AD与CM交于点E,若⊙O的半径为2,ED=1,求AC的长.
分析 (1)连接OC,由∠ABC+∠BAC=90°及CM是⊙O的切线得出∠ACM+∠ACO=90°,再利用∠BAC=∠ACO,得出结论,
(2)连接OC,得出△AEC是直角三角形,△AEC的外接圆的直径是AC,利用△ABC∽△CDE,求出AC.
解答 (1)证明:连接OC.
∵AB为⊙O的直径,
∴∠ACB=90°.
∴∠ABC+∠BAC=90°.
∵CM是⊙O的切线,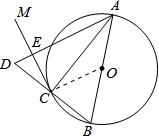
∴OC⊥CM.
∴∠ACM+∠ACO=90°.
∵CO=AO,
∴∠BAC=∠ACO.
∴∠ACM=∠ABC.
(2)解:∵BC=CD,OB=OA,
∴OC∥AD.
又∵OC⊥CE,
∴CE⊥AD,
∵∠ACD=∠ACB=90°,
∴∠AEC=∠ACD.
∴△ADC∽△ACE.
∴$\frac{AD}{AC}=\frac{AC}{AE}$.
∵⊙O的半径为2,
∴AD=4.
∴$\frac{4}{AC}=\frac{AC}{3}$.
∴AC=2$\sqrt{3}$.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.也考查了勾股定理、圆周角定理和相似三角形的判定与性质.解题的关键是找准角的关系.

练习册系列答案
相关题目
9.若关于x的一元二次方程ax2+3x+1=0有实数根,则a的取值范围( )
| A. | a<$\frac{9}{4}$ | B. | a≤$\frac{9}{4}$ | C. | a≥$\frac{9}{4}$ | D. | a≤$\frac{9}{4}$且a≠0 |
7.若把代数式x2-2x+3化为(x-m)2+k形式,其中m,k为常数,结果为( )
| A. | (x+1)2+4 | B. | (x-1)2+2 | C. | (x-1)2+4 | D. | (x+1)2+2 |
8. 如图,AB∥CD,∠D=13°,∠B=28°,那么∠E等于( )
如图,AB∥CD,∠D=13°,∠B=28°,那么∠E等于( )
 如图,AB∥CD,∠D=13°,∠B=28°,那么∠E等于( )
如图,AB∥CD,∠D=13°,∠B=28°,那么∠E等于( )| A. | 13° | B. | 14° | C. | 15° | D. | 16° |
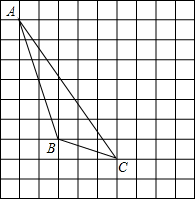 如图,每个小正方形的边长为1个单位.
如图,每个小正方形的边长为1个单位.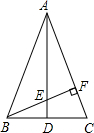 如图,在△ABC中,AB=AC,D为BC的中点,∠BAC=45°,BF⊥AC交AD,求证:CF=EF.
如图,在△ABC中,AB=AC,D为BC的中点,∠BAC=45°,BF⊥AC交AD,求证:CF=EF.