题目内容
9.关于x的一元二次方程x2+3x-m=0有两个不相等的实数根,则实数m的取值范围是m>-$\frac{9}{4}$.分析 根据一元二次方程x2+3x-m=0有两个不相等的实数根可得△=32-4(-m)>0,求出m的取值范围即可.
解答 解:∵一元二次方程x2+3x-m=0有两个不相等的实数根,
∴△=32-4(-m)>0,
∴m>-$\frac{9}{4}$,
故答案为m>-$\frac{9}{4}$.
点评 本题主要考查了根的判别式的知识,解答本题的关键是掌握一元二次方程根的情况与判别式△的关系:△>0?方程有两个不相等的实数根,此题难度不大.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
20.同学们都知道,蜜蜂建造的蜂巢既坚固又省料,那你知道蜂巢的厚度吗?事实上,蜂巢厚度约为0.000073m,此数用科学记数法表示为( )
| A. | 7.3×10-4m | B. | 7.3×10-5m | C. | 7.3×105m | D. | 73×10-5m |
4.正五边形的每个外角等于( )
| A. | 36° | B. | 60° | C. | 72° | D. | 108° |
1. 如图,数轴上两点A,B表示的数互为相反数,则点B表示的数为( )
如图,数轴上两点A,B表示的数互为相反数,则点B表示的数为( )
 如图,数轴上两点A,B表示的数互为相反数,则点B表示的数为( )
如图,数轴上两点A,B表示的数互为相反数,则点B表示的数为( )| A. | -1 | B. | 1 | C. | -2 | D. | 2 |
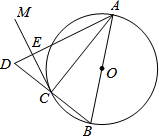 如图,AB是⊙O的直径,点C在⊙O上,过点C作⊙O的切线CM.
如图,AB是⊙O的直径,点C在⊙O上,过点C作⊙O的切线CM.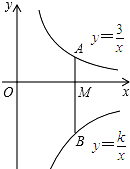 如图,点A在函数y=$\frac{3}{x}$(x>0)的图象上,点B在函数y=$\frac{k}{x}$(x>0)的图象上,连接AB,AB垂直x轴于点M,且AM:MB=1:2,则k=-6.
如图,点A在函数y=$\frac{3}{x}$(x>0)的图象上,点B在函数y=$\frac{k}{x}$(x>0)的图象上,连接AB,AB垂直x轴于点M,且AM:MB=1:2,则k=-6.