题目内容
11.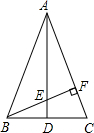 如图,在△ABC中,AB=AC,D为BC的中点,∠BAC=45°,BF⊥AC交AD,求证:CF=EF.
如图,在△ABC中,AB=AC,D为BC的中点,∠BAC=45°,BF⊥AC交AD,求证:CF=EF.
分析 根据垂直定义和三角形的内角和定理求出∠ABF=∠BAF=45°,根据等腰三角形性质得出BF=AF,求出∠CBF=∠EAF,∠BFC=∠AFE=90°,根据AAS推出△EAF≌△CBF即可.
解答 证明:∵BF⊥AC,
∴∠BFA=90°,
∵∠BAC=45°,
∴∠ABF=∠BAF=45°,
∴BF=AF,
∵AD⊥BC,BF⊥AC,
∴∠BDF=∠BFA=90°,
∴∠FAE+∠AEF=90°,∠CBF+∠BED=90°,
∵∠BED=∠AEF,
∴∠CBF=∠EAF,
∵BF⊥AC,
∴∠BFC=∠AFE=90°,
在△EAF和△CBF中,
$\left\{\begin{array}{l}{∠AFE=∠BFC}\\{∠EAF=∠CBF}\\{AF=BF}\end{array}\right.$,
∴△EAF≌△CBF(AAS),
∴EF=CF.
点评 本题考查了全等三角形的性质和判定,等腰三角形的判定,三角形内角和定理,垂直定义的应用,解此题的关键是推出△EAF≌△CBF,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS,全等三角形的对应边相等,对应角相等.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
1.$\sqrt{81}$的平方根是( )
| A. | 9 | B. | 3 | C. | ±9 | D. | ±3 |
2.$\frac{2}{3}$的倒数是( )
| A. | $-\frac{2}{3}$ | B. | $\frac{2}{3}$ | C. | $-\frac{3}{2}$ | D. | $\frac{3}{2}$ |
6.下面的性质中,平行四边形不一定具有的是( )
| A. | 内角和为360° | B. | 邻角互补 | C. | 对角相等 | D. | 对角互补 |
20.同学们都知道,蜜蜂建造的蜂巢既坚固又省料,那你知道蜂巢的厚度吗?事实上,蜂巢厚度约为0.000073m,此数用科学记数法表示为( )
| A. | 7.3×10-4m | B. | 7.3×10-5m | C. | 7.3×105m | D. | 73×10-5m |
1. 如图,数轴上两点A,B表示的数互为相反数,则点B表示的数为( )
如图,数轴上两点A,B表示的数互为相反数,则点B表示的数为( )
 如图,数轴上两点A,B表示的数互为相反数,则点B表示的数为( )
如图,数轴上两点A,B表示的数互为相反数,则点B表示的数为( )| A. | -1 | B. | 1 | C. | -2 | D. | 2 |
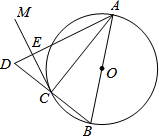 如图,AB是⊙O的直径,点C在⊙O上,过点C作⊙O的切线CM.
如图,AB是⊙O的直径,点C在⊙O上,过点C作⊙O的切线CM. 如图,已知直线y=$\frac{1}{2}$x与双曲线y=$\frac{k}{x}$(k>0)交于两点,且点A的横坐标为2,
如图,已知直线y=$\frac{1}{2}$x与双曲线y=$\frac{k}{x}$(k>0)交于两点,且点A的横坐标为2,