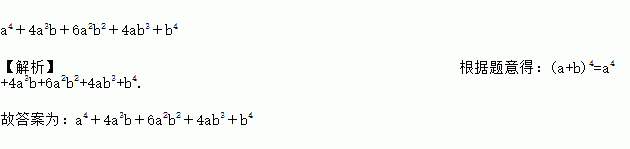题目内容
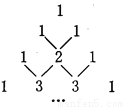
如图是我国古代数学家杨辉最早发现的图形，称为“杨辉三角”．他的发现比西方要早五百年左右，由此可见我国古代数学的成就是非常值得中华民族自豪的！“杨辉三角”中有许多规律，如其中每一行的数字正好对应了（a＋b）n（n为非负整数）的展开式中a按次数从大到小排列的项的系数．例如，(a＋b)2＝a2＋2ab＋b2，展开式中的系数1、2、1恰好对应图中第三行的数字；再如，(a＋b)3＝a3＋3a2b＋3ab2＋b3，展开式中的系数1、3、3、1恰好对应图中第四行的数字．请认真观察此图，写出（a＋b)4的展开式，(a＋b)4＝_______．
a4＋4a3b＋6a2b2＋4ab3＋b4
【解析】根据题意得：(a+b)4=a4+4a3b+6a2b2+4ab3+b4.
故答案为：a4＋4a3b＋6a2b2＋4ab3＋b4
天天向上一本好卷系列答案
小学生10分钟应用题系列答案在△ABC中，∠C＝90°，cosA＝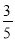
，AC＝6.求△ABC的周长和面积．
周长为24，面积为24.
【解析】试题分析：根据余弦的定义求出斜边AB的长，再根据勾股定理求出BC的长，再根据三角形的周长、面积的求法即可得.
试题解析：∵∠C=90°，∴cosA=，
∵cosA＝，AC＝6，
∴AB=10，
∴BC==8，
∴△ABC的周长=AC+BC+AB=6+8+10=24，
S△ABC==24. 下列命题正确的是（ ）
A．内错角相等
B．相等的角是对顶角
C．三条直线相交 ，必产生同位角、内错角、同旁内角
D．同位角相等，两直线平行
D．
【解析】
试题分析：A．只有两直线平行，内错角才相等，故错误；
B．对顶角相等，但相等的角不一定是对顶角，故错误；
C．必须出现“三线八角”的形式，即两直线被第三条直线所截，才产生同位角，内错角，同旁内角，故错误；
D．平行线的判定定理，故正确．
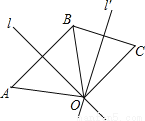
故选D． 如图，l是线段AB的对称轴，l′是线段BC的对称轴，l和l′相交于点O．OA与OC相等吗？为什么？
相等，理由见解析
【解析】试题分析：由轴对称的性质即可证明．
试题解析：【解析】
∵l是线段AB的对称轴，∴OA=OB，
∵l′是线段BC的对称轴，∴OB=OC，
∴OA=OC． 下列语句中，正确的个数有（ ）
①两个关于某直线对称的图形是全等的
②两个图形关于某直线对称，对称点一定在该直线的两旁
③两个成轴对称的图形的对应点连线的垂直平分线，就是它们的对称轴
④平面内两个全等的图形一定关于某直线对称．
A. 1个 B. 2个 C. 3个 D. 4个
B
【解析】【解析】
①两个关于某直线对称的图形是全等的，此选项正确；
②两个图形关于某直线对称，对称点一定在该直线的两旁也有可能在直线上，此选项错误；
③两个成轴对称的图形的对应点连线的垂直平分线，就是它们的对称轴，此选项正确；
④平面内两个全等的图形不一定关于某直线对称，故此选项错误．
故选B． 计算:
(1)-23+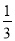
(2017+3)0-
;
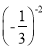(2)992-69×71;
(3)(-2+x)(-2-x);
(4)(m+2)2(m-2)2(m2+4)2;
(5)(a+b-c)(a-b+c);
(6)(3x-2y+1)2.
(1)-16 (2)4902(3)4-x2(4)m8-32m4+256(5)a2-b2-c2+2bc(6) 9x2+4y2-12xy+6x-4y+1
【解析】试题分析：（1）根据实数的运算顺序依次计算即可；（2）把99化为100-1，把69化为70-1,71化为70+1，再利用完全平方公式和平方差公式进行计算即可；（3）直接利用平方差公式计算即可；（4）逆用积的乘方的运算法则后利用平方差公式... 若(3x+1)-3有意义,则x的取值范围是___________.
x≠-
【解析】(3x+1)-3= ，根据分式有意义的条件可得3x+1≠0，即. ΔABC和ΔA’B’C’关于直线l对称，若ΔABC的周长为12cm，ΔA’B’C’的面积为6cm2,则ΔA’B’C’的周长为___________，ΔABC的面积为_________.
12cm 6cm2
【解析】【解析】
成轴对称的两个图形全等，所以周长相等，面积相等．故答案为：12cm，6cm2． 生物学研究表明，在8﹣﹣17岁期间，男女生身高增长速度规律呈现如下图所示，请你观察此图，回答下列问题，男生身高增长速度的巅峰是几岁？在几岁时男生、女生的身高增长速度是一样的？
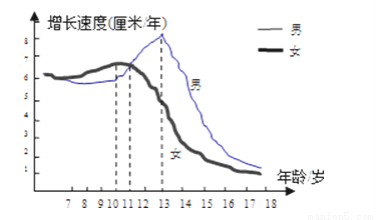
见解析
【解析】试题分析：结合图形观察男生女生的增长线图的最高点即是身高增长速度的巅峰，两身高线的交点就是他们的增长速度一样．
试题解析：男生身高增长速度的巅峰是13岁，在11岁时男生、女生身高增长速度是一样的。