题目内容
设抛物线y=ax2+bx+c与x轴交于A,B两点,在抛物线上取点C,使∠ACB=90°,那么b2-4ac的取值范围是 .
考点:抛物线与x轴的交点
专题:
分析:设A、B点坐标分别为x1、x2,求出用x1、x2表示的AB长度的表达式;求出抛物线顶点纵坐标表达式,根据顶点的纵坐标的绝对值大于或等于
AB的关系得到关系式;将b2-4ac看做一个整体,解不等式即可得到正确答案.
| 1 |
| 2 |
解答:解:设A、B点坐标分别为x1、x2,
则AB=|x1-x2|=
=
=
;
抛物线顶点坐标为(-
,
),
∵∠ACB=90°,
∴以AB为直径作圆与抛物线的交点即为C点,
∴|
|≥
×
,
两边平方得,
≥
,
去分母得,(b2-4ac)2≥4(b2-4ac),
∵抛物线y=ax2+bx+c与x轴交于A,B两点,
∴b2-4ac>0,
∴b2-4ac≥4.
则AB=|x1-x2|=
| (x1+x2)2-4x1x2 |
(-
|
| ||
| |a| |
抛物线顶点坐标为(-
| b |
| 2a |
| 4ac-b2 |
| 4a |
∵∠ACB=90°,
∴以AB为直径作圆与抛物线的交点即为C点,
∴|
| 4ac-b2 |
| 4a |
| 1 |
| 2 |
| ||
| |a| |
两边平方得,
| (b2-4ac)2 |
| 16a2 |
| b-4ac |
| 4a2 |
去分母得,(b2-4ac)2≥4(b2-4ac),
∵抛物线y=ax2+bx+c与x轴交于A,B两点,
∴b2-4ac>0,
∴b2-4ac≥4.
点评:此题考查了抛物线与x轴的交点横坐标与两点间的距离的关系、抛物线顶点坐标及抛物线上点的坐标特征,根据已知得出顶点的纵坐标的绝对值大于或等于
AB的关系是本题的关键.
| 1 |
| 2 |

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
下列说法正确的是( )
A、若x=y,则
| ||||
| B、若|a|=-a,则a<0 | ||||
| C、若a,b互为相反数,那么a,b的商必定等于-1 | ||||
| D、若关于x的方程2x-1=3与3x-2a=0的解相同,则a=3 |
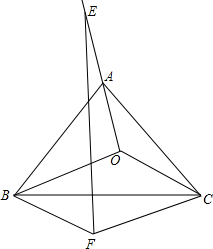 已知O是等边三角形ABC所在平面上任意一点,连接OA并延长到E,使得AE=OA,以OB,OC为邻边作平行四边形OBFC连接EF,请探索FE与BC之间的关系.
已知O是等边三角形ABC所在平面上任意一点,连接OA并延长到E,使得AE=OA,以OB,OC为邻边作平行四边形OBFC连接EF,请探索FE与BC之间的关系. 如图,已知点D是⊙O外的一点,DA为⊙O的切线,A为切点,AB为⊙O的直径,BD交⊙O于点C,若DA=4,DC=2,求图中阴影部分面积.
如图,已知点D是⊙O外的一点,DA为⊙O的切线,A为切点,AB为⊙O的直径,BD交⊙O于点C,若DA=4,DC=2,求图中阴影部分面积. 已知一个立体图形的三视图如图所示,现沿它的同一顶点的三条棱将其剪开展成平面图形,则所得到的平面展开图是下列图中的( )
已知一个立体图形的三视图如图所示,现沿它的同一顶点的三条棱将其剪开展成平面图形,则所得到的平面展开图是下列图中的( )



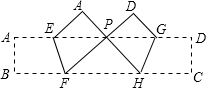 把长方形纸条ABCD沿EF,GH同时折叠,B、C两点恰好都落在AD边的P点处,若∠FPH=90°,PF=8,PH=6,则长方形ABCD的面积为多少?
把长方形纸条ABCD沿EF,GH同时折叠,B、C两点恰好都落在AD边的P点处,若∠FPH=90°,PF=8,PH=6,则长方形ABCD的面积为多少? 某工厂要赶制一批抗震救灾用的大型活动板房,如图,板房一面的形状是由矩形和抛物线的一部分组成,矩形长为12m,抛物线拱高为3.6m.
某工厂要赶制一批抗震救灾用的大型活动板房,如图,板房一面的形状是由矩形和抛物线的一部分组成,矩形长为12m,抛物线拱高为3.6m.