题目内容
 已知抛物线y=-
已知抛物线y=-| 1 |
| 4 |
考点:二次函数图象上点的坐标特征
专题:计算题
分析:作CD⊥x轴于D,如图,先证明Rt△ABO∽Rt△CAD,利用相似比得到CD=2AD,再根据二次函数图象上点的坐标特征,设C(t,-
t2+t-1),所以-(-
t2+t-1)=2(t-2),解得t1=2
+6,t2=-2
+6(舍去),于是可得到C点坐标.
| 1 |
| 4 |
| 1 |
| 4 |
| 6 |
| 6 |
解答:解: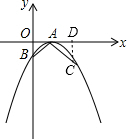 作CD⊥x轴于D,如图,
作CD⊥x轴于D,如图,
∵A(2,0),B(0,-1),
∴OA=2,OB=1,
∵AB⊥AC,
∴∠OAB+∠CAD=90°,
而∠OAB+∠ABO=90°,
∴∠ABO=∠CAD,
∴Rt△ABO∽Rt△CAD,
∴
=
,即
=
,
∴CD=2AD,
设C(t,-
t2+t-1),
∴-(-
t2+t-1)=2(t-2),
整理得t2+12t-20=0,解得t1=2
+6,t2=-2
+6(舍去),
∴C点坐标为(2
+6,-8-4
).
 作CD⊥x轴于D,如图,
作CD⊥x轴于D,如图,∵A(2,0),B(0,-1),
∴OA=2,OB=1,
∵AB⊥AC,
∴∠OAB+∠CAD=90°,
而∠OAB+∠ABO=90°,
∴∠ABO=∠CAD,
∴Rt△ABO∽Rt△CAD,
∴
| OA |
| CD |
| OB |
| AD |
| 2 |
| CD |
| 1 |
| AD |
∴CD=2AD,
设C(t,-
| 1 |
| 4 |
∴-(-
| 1 |
| 4 |
整理得t2+12t-20=0,解得t1=2
| 6 |
| 6 |
∴C点坐标为(2
| 6 |
| 6 |
点评:本题考查了二次函数图象上点的坐标特征:二次函数图象上点的坐标满足其解析式.也考查了相似三角形的判定与性质.

练习册系列答案
相关题目
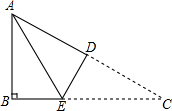 如图所示,在△ABC中,∠B=90°,AB=3,AC=5,将△ABC折叠,使点C与点A重合,折痕为DE,则BE的长为( )
如图所示,在△ABC中,∠B=90°,AB=3,AC=5,将△ABC折叠,使点C与点A重合,折痕为DE,则BE的长为( )A、
| ||
B、
| ||
C、
| ||
D、
|
 如图所示,∠AOP=∠BOP=15°,PC∥OA,PD⊥OA于D,若PC=8,则PD=( )
如图所示,∠AOP=∠BOP=15°,PC∥OA,PD⊥OA于D,若PC=8,则PD=( )| A、3 | B、4 | C、5 | D、6 |
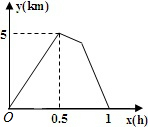 甲、乙二人同时从A地到B地,甲骑自行车,乙步行,甲到B地后休息了十分钟然后以相同的速度返回,在返回途中与乙相遇,甲、乙二人之间的距离y(km)与乙步行时间x(h)之间的关系如图,则甲从出发到返回与乙相遇共走了
甲、乙二人同时从A地到B地,甲骑自行车,乙步行,甲到B地后休息了十分钟然后以相同的速度返回,在返回途中与乙相遇,甲、乙二人之间的距离y(km)与乙步行时间x(h)之间的关系如图,则甲从出发到返回与乙相遇共走了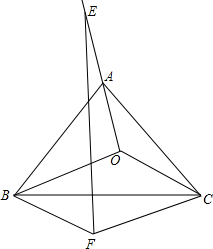 已知O是等边三角形ABC所在平面上任意一点,连接OA并延长到E,使得AE=OA,以OB,OC为邻边作平行四边形OBFC连接EF,请探索FE与BC之间的关系.
已知O是等边三角形ABC所在平面上任意一点,连接OA并延长到E,使得AE=OA,以OB,OC为邻边作平行四边形OBFC连接EF,请探索FE与BC之间的关系. 已知一个立体图形的三视图如图所示,现沿它的同一顶点的三条棱将其剪开展成平面图形,则所得到的平面展开图是下列图中的( )
已知一个立体图形的三视图如图所示,现沿它的同一顶点的三条棱将其剪开展成平面图形,则所得到的平面展开图是下列图中的( )



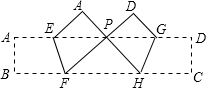 把长方形纸条ABCD沿EF,GH同时折叠,B、C两点恰好都落在AD边的P点处,若∠FPH=90°,PF=8,PH=6,则长方形ABCD的面积为多少?
把长方形纸条ABCD沿EF,GH同时折叠,B、C两点恰好都落在AD边的P点处,若∠FPH=90°,PF=8,PH=6,则长方形ABCD的面积为多少?