题目内容
16.将函数y=x2-2x-3的图象沿y轴翻折后与原图象合起来,构成一个新的函数的图象,若y=m与新图象有四个公共点,则m的取值范围为m>-4且m≠-3.分析 先根据函数解析式画出图形,然后结合图形可求得取值范围.
解答 解:翻折后所得新图象如图所示.
∵函数y=x2-2x-3=(x-1)2-4,
∴顶点P的坐标为(1,-4),
∴Q(-1,-4),
当直线y=m经过Q(-1,-4)时,m=-3,
∴此时直线与新图象有32个交点,且经过点(0,-3),
∵翻折后的抛物线y=(x+1)2-4,
由$\left\{\begin{array}{l}{y=m}\\{y=(x+1)^{2}-4}\end{array}\right.$
消去y得x2+2x-3-m=0,
当△=0时,4+4(3+m)=0,
m=-4时,直线y=m与新图象有两个交点,
当m=-3时,直线y=m与新图象有三个交点,
∴若直线y=m与新图象有四个公共点,则m的取值范围为m>-4且m≠-3,故答案为:m>-4且m≠-3.
点评 本题考查了二次函数和y轴的交点问题,平移的性质,二次函数的图象与几何变换的应用,主要考查学生的理解能力,题目比较好,有一定的难度.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
6.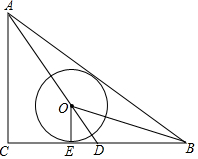 如图,△ABC中,∠C=90°,AC=3,AB=5,点O在BC边的中线AD上,⊙O与BC相切于点E,且∠OBA=∠OBC.
如图,△ABC中,∠C=90°,AC=3,AB=5,点O在BC边的中线AD上,⊙O与BC相切于点E,且∠OBA=∠OBC.
(1)求证:AB为⊙O的切线;
(2)求⊙O的半径;
(3)求tan∠BAD.
 如图,△ABC中,∠C=90°,AC=3,AB=5,点O在BC边的中线AD上,⊙O与BC相切于点E,且∠OBA=∠OBC.
如图,△ABC中,∠C=90°,AC=3,AB=5,点O在BC边的中线AD上,⊙O与BC相切于点E,且∠OBA=∠OBC.(1)求证:AB为⊙O的切线;
(2)求⊙O的半径;
(3)求tan∠BAD.
4. 如图,将长8cm,宽4cm的矩形纸片ABCD折叠,使点A与C重合,则四边形AECF的周长为( )
如图,将长8cm,宽4cm的矩形纸片ABCD折叠,使点A与C重合,则四边形AECF的周长为( )
 如图,将长8cm,宽4cm的矩形纸片ABCD折叠,使点A与C重合,则四边形AECF的周长为( )
如图,将长8cm,宽4cm的矩形纸片ABCD折叠,使点A与C重合,则四边形AECF的周长为( )| A. | 12 cm | B. | 16 cm | C. | 20 cm | D. | 24 cm |
11.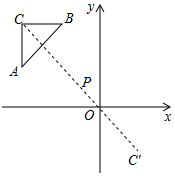 如图,△ABC的顶点坐标分别为A(-4,2),B(-2,4),C(-4,4),以点P(-1,1)为位似中心,将△ABC缩小后得到△A′B′C′.若点C的对应点C′的坐标为(2,-2),则点A的对应点A′的坐标为( )
如图,△ABC的顶点坐标分别为A(-4,2),B(-2,4),C(-4,4),以点P(-1,1)为位似中心,将△ABC缩小后得到△A′B′C′.若点C的对应点C′的坐标为(2,-2),则点A的对应点A′的坐标为( )
 如图,△ABC的顶点坐标分别为A(-4,2),B(-2,4),C(-4,4),以点P(-1,1)为位似中心,将△ABC缩小后得到△A′B′C′.若点C的对应点C′的坐标为(2,-2),则点A的对应点A′的坐标为( )
如图,△ABC的顶点坐标分别为A(-4,2),B(-2,4),C(-4,4),以点P(-1,1)为位似中心,将△ABC缩小后得到△A′B′C′.若点C的对应点C′的坐标为(2,-2),则点A的对应点A′的坐标为( )| A. | (2,0) | B. | (2,-1) | C. | (0,-2) | D. | (1,-2) |
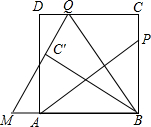 如图,P为正方形ABCD的边BC上一点,连接AP,过点B作BQ⊥AP,交CD于点Q,将△BQC沿BQ所在的直线对折得到△BQC′,延长QC′,交BA的延长线于点M,当AB=3,BP=2PC时,QM=$\frac{13}{4}$.
如图,P为正方形ABCD的边BC上一点,连接AP,过点B作BQ⊥AP,交CD于点Q,将△BQC沿BQ所在的直线对折得到△BQC′,延长QC′,交BA的延长线于点M,当AB=3,BP=2PC时,QM=$\frac{13}{4}$.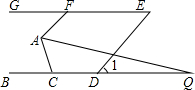 如图,已知BC∥GE,AF∥DE,∠EDQ=50°.若AQ平分∠FAC,交BC于点Q,且∠Q=15°,则∠ACB的度数为80°.
如图,已知BC∥GE,AF∥DE,∠EDQ=50°.若AQ平分∠FAC,交BC于点Q,且∠Q=15°,则∠ACB的度数为80°.