题目内容
某商场计划购进一批甲、乙两种玩具,已知一件甲种玩具的进价与一件乙种玩具的进价的和为50元,用90元购进甲种玩具的件数与用210元购进乙种玩具的件数相同.
(1)求每件甲种、乙种玩具的进价分别是多少元?
(2)商场计划购进甲、乙两种玩具共40件,其中甲种玩具的件数不多于乙种玩具的件数的4倍,为了节约经费,应购买甲、乙两种玩具各多少件?使用经费最少为多少元?
(1)求每件甲种、乙种玩具的进价分别是多少元?
(2)商场计划购进甲、乙两种玩具共40件,其中甲种玩具的件数不多于乙种玩具的件数的4倍,为了节约经费,应购买甲、乙两种玩具各多少件?使用经费最少为多少元?
考点:分式方程的应用,一元一次不等式的应用
专题:
分析:(1)设甲玩具的进价是x元,则乙玩具的进价为(50-x)元,根据用90元购进甲种玩具的件数与用210元购进乙种玩具的件数相同建立方程求出其解即可;
(2)设甲种玩具购进a件,则乙种玩具购进(40-a)件,需要的总费用为W元,根据总费用=两种玩具的费用之和表示出W与a之间的函数关系式,由一次函数的性质就可以求出结论.
(2)设甲种玩具购进a件,则乙种玩具购进(40-a)件,需要的总费用为W元,根据总费用=两种玩具的费用之和表示出W与a之间的函数关系式,由一次函数的性质就可以求出结论.
解答:解:(1)设甲玩具的进价是x元,则乙玩具的进价为(50-x)元,由题意,得
=
,
解得:x=15,
经检验,x=15是原方程的解,且符合题意.
∴乙种玩具的进价为:50-15=35元.
答:甲玩具的进价是15元,则乙玩具的进价为35元;
(2)设甲种玩具购进a件,则乙种玩具购进(40-a)件,需要的总费用为W元,由题意,得
W=15a+35(40-a)=-20a+1400,
∴k=-20<0,
∴W随a的增大而减小.
∵a≤4(40-a)
∴a≤32.
∴a=32时,
W最小=-20×32+1400=760元.
| 90 |
| x |
| 210 |
| 50-x |
解得:x=15,
经检验,x=15是原方程的解,且符合题意.
∴乙种玩具的进价为:50-15=35元.
答:甲玩具的进价是15元,则乙玩具的进价为35元;
(2)设甲种玩具购进a件,则乙种玩具购进(40-a)件,需要的总费用为W元,由题意,得
W=15a+35(40-a)=-20a+1400,
∴k=-20<0,
∴W随a的增大而减小.
∵a≤4(40-a)
∴a≤32.
∴a=32时,
W最小=-20×32+1400=760元.
点评:本题考查了列分时方程解实际问题的运用,分时方程的解法的运用,一次函数的解析式的性质的运用,解答时求出一次函数的解析式是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
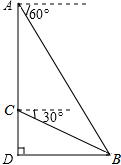 如图,哨兵在灯塔顶部A处测得遇难船只所在地B处的俯角为60°,然后下到灯塔的C处,测得B处的俯角为30°.已知AC=40米,若救援船只以5m/s 的速度从灯塔底部D处出发,几秒钟后能到达遇难船只的位置?(结果精确到个位).
如图,哨兵在灯塔顶部A处测得遇难船只所在地B处的俯角为60°,然后下到灯塔的C处,测得B处的俯角为30°.已知AC=40米,若救援船只以5m/s 的速度从灯塔底部D处出发,几秒钟后能到达遇难船只的位置?(结果精确到个位).
 如图,在方格纸上建立平面直角坐标系,每个小正方形的边长为1.
如图,在方格纸上建立平面直角坐标系,每个小正方形的边长为1.