题目内容

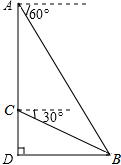如图，哨兵在灯塔顶部A处测得遇难船只所在地B处的俯角为60°，然后下到灯塔的C处，测得B处的俯角为30°．已知AC=40米，若救援船只以5m/s 的速度从灯塔底部D处出发，几秒钟后能到达遇难船只的位置？（结果精确到个位）．
考点：解直角三角形的应用-仰角俯角问题
专题：
分析：在Rt△BCD中，先求得BD=
3
CD．在Rt△ABD中，
AD
BD
=tan60°，解得：CD=20．再求时间即可．
解答：解：在Rt△BCD中
∵∠BCD=90°-30°=60°，
∴
BD
CD
=tan60°，则BD=
3
CD．
在Rt△ABD中，
∵∠ABD=60°，
∴
AD
BD
=tan60°．
即
40+CD
3
CD
=
3

解得：CD=20．
∴t=
3
CD
5
=
35
3
=7s．
故约7s后能到达遇难船只的位置．
点评：本题主要考查了解直角三角形的应用-仰角俯角问题．关键是求得CD的长．
练习册系列答案
相关题目
如图，已知长方形相邻两边的长分别是x cm和4cm，设长方形的周长为y cm．
（1）试写出长方形的周长y与x之间的关系式；
（2）利用（1）中的关系式，求x与10cm时长方形的周长；
（3）利用（1）中的关系式，求周长为30cm时x的值．
某校初三（1）班团支部组织班级全体团员参加校团委组织的“中国梦”写短信比赛活动．团支部对该班全体团员所发短信条数的情况进行了统计，并制成了如下两幅不完整的统计图：
（1）求该班团员共有多少人？请将条形统计图补充完整，并求出平均每人发短信多少条？
（2）经调查，发了3条短信的同学中有两位男同学，发了4条短信的同学中有三位女同学．现要从发了3条短信和4条短信的同学中各选出一位参加该次活动的表彰总结会，请你用画树状图或列表的方法求所选两位同学中恰好是一位男同学和一位女同学的概率．
已知抛物线y=-x2+2mx-m2+1与x轴交点为A、B（点B在点A的右侧），与y轴交于点C．
（1）试用含m的代数式表示A、B两点的坐标；
（2）当点B在原点的右侧，点C在原点的下方时，若△BOC是等腰三角形，求抛物线的解析式；
（3）已知一次函数y=kx+b，点P（n，0）是x轴上一个动点，在（2）的条件下，过点P作垂直于x轴的直线交这个一次函数的图象于点M，交抛物线y=-x2+2mx-m2+1于点N，若只有当1＜n＜4时，点M位于点N的下方，求这个一次函数的解析式．
在对口扶贫活动中，企业甲将经营状况良好的某消费品专卖店，以5.8万元的优惠价转让给了尚有5万元无息贷款还没有偿还的小型残疾人企业乙，并约定从该店经营的利润中，首先保证企业乙的全体职工每月最低生活费的开支4000元后，逐步偿还转让费（不计利息）从企业甲提供的相关资料中可知这种消费品的进价是每件12元；月销售量Q（百件）与销售单价P（元）的关系如图所示，但销售量受市场需求量的限制，维持企业的正常运转每月需最低生活费外的各种开支2000元．
（1）试确定月销售量Q（百件）与销售单价P（元）的关系关系式；
（2）当商品的销售单价为多少元时，月利润最大？
（3）企业乙依靠该店，最早可在几年内脱贫？
观察下列等式：
①
1
2
+1
=
2
-1
(
2
+1)(
2
-1)
=
2
-1；
②
1
3
+
2
=
3
-
2
(
3
+
2
)(
3
-
2
)
=
3
-
2
；
③
1
4
+
3
=
4
-
3
(
4
+
3
)(
4
-
3
)
=
4
-
3
；
…
回答下列问题：
（1）仿照上列等式，写出第n个等式：
 
；
（2）利用你观察到的规律，化简：
1
2
3
+
11
；
（3）计算：
1
1+
2
+
1
2
+
3
+
1
3
+2
+…+
1
3+
10
．
如图，在?ABCD中，E为BC的中点，连接AE并延长交DC的延长线于点F，连接BF、AC，求证：AC=BF．
某商场计划购进一批甲、乙两种玩具，已知一件甲种玩具的进价与一件乙种玩具的进价的和为50元，用90元购进甲种玩具的件数与用210元购进乙种玩具的件数相同．
（1）求每件甲种、乙种玩具的进价分别是多少元？
（2）商场计划购进甲、乙两种玩具共40件，其中甲种玩具的件数不多于乙种玩具的件数的4倍，为了节约经费，应购买甲、乙两种玩具各多少件？使用经费最少为多少元？
剧院里5排3号可以用（5，3）表示，则8排6号用
 
表示．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网