题目内容
14.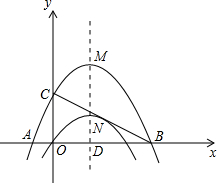 已知:如图二次函数y=-$\frac{1}{4}$x2+bx+c图象经过原点O,图象顶点为N,对称轴ND为直线x=3.
已知:如图二次函数y=-$\frac{1}{4}$x2+bx+c图象经过原点O,图象顶点为N,对称轴ND为直线x=3.(1)求此二次函数表达式;
(2)将该抛物线沿它的对称轴向上平移到点M,设平移后的抛物线与x轴,y轴的交点分别为A、B、C三点,连结AC、AB、BC,当tan∠ABC=$\frac{1}{2}$,求证:△ABC是直角三角形;
(3)在(2)的基础上,试求出以线段OC、MN和两抛物线所围成的区域的面积.
分析 (1)根据对称轴公式,待定系数法,可得函数关系式;
(2)根据正切函数,可得B点坐标,根据待定系数法,可得平移后的解析式,根据正切值,可得∠ABC=∠ACO,根据余角的性质,可得答案;
(3)根据线段CM与平移后的抛物线围成区域和线段ON与原抛物线围成的区域面积相等,可得以线段OC、MN和两抛物线所围成的区域的面积等于S四边形OCNM.
解答 解:(1)由图象经过原点,得
c=0,由对称轴等于3,得
x=-$\frac{b}{-2×\frac{1}{4}}$=3,解得b=$\frac{3}{2}$,
y=-$\frac{1}{4}$x2+$\frac{3}{2}$x;
(2)设平移后的抛物线y=-$\frac{1}{4}$x2+$\frac{3}{2}$x+c,则OC=c,tan∠ABC=$\frac{1}{2}$,
∴OB=2c,则B点坐标为(2c,0),
把点B代入上式,得c=4,
∴平移后的抛物线y=-$\frac{1}{4}$x2+$\frac{3}{2}$x+4,
∵OA=2,OC=4,OB=8,tan∠ABC=tan∠ACO=$\frac{1}{2}$,
∴∠ABC=∠ACO,
∵OC⊥AB,
∴∠ABC+∠BCO=90°,
∴∠ACO+∠BCO=90°,
∴∠ACB=90°,
∴△ABC是直角三角形;
(3)如图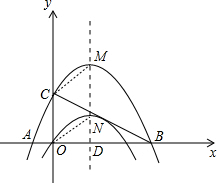 ,
,
连线CM,ON,由平移,得
OC平行且等于MN,
∴四边形OCNM是平行四边形,S四边形OCNM=OC•OD=12,
由平移,得
线段CM与平移后的抛物线围成区域和线段ON与原抛物线围成的区域面积相等,
则以线段OC、MN和两抛物线所围成的区域的面积等于S四边形OCNM=12.
点评 本题考查了二次函数综合题,解(1)的关键是待定系数法;解(2)的关键是利用正切函数的定义得出∠ABC=∠ACO,又利用了余角的性质;解(3)的关键是利用平移得出以线段OC、MN和两抛物线所围成的区域的面积等于S四边形OCNM.

 如图,已知△ABC≌△DEF,点B,E,C,F在同一条直线上,若BC=5,BE=2,则BF=7.
如图,已知△ABC≌△DEF,点B,E,C,F在同一条直线上,若BC=5,BE=2,则BF=7. 如图,在△ABC中,D、E分别是AB、BC上的点,且DE∥AC,若BE:BC=1:4,则S△BDE:S△ACD的比为1:12.
如图,在△ABC中,D、E分别是AB、BC上的点,且DE∥AC,若BE:BC=1:4,则S△BDE:S△ACD的比为1:12.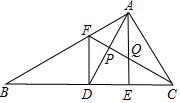 如图,D为△ABC中边BC中点,E为CD上一点,将△ACE沿AE折叠时C与D重合,F为AB上一点,FB=FC,FC与AD、AE分别交于P、Q点,下列结论
如图,D为△ABC中边BC中点,E为CD上一点,将△ACE沿AE折叠时C与D重合,F为AB上一点,FB=FC,FC与AD、AE分别交于P、Q点,下列结论