题目内容
若三个非负数a、b、c满足2a+3b+c=10,2a+b-c=2,且m=3a+b+c,则m的最大值与最小值的和是 .
考点:解一元一次不等式组,解二元一次方程组
专题:
分析:首先解2a+3b+c=10和2a+b-c=2组成的关于a、b的方程组,根据c是非负数即可求得c的范围,即可求得m的范围.
解答:解:解关于a、b的方程组
,
解得:
,
根据题意得:
,
解得:1≤c≤4.
则m=3a+b+c=3(c-1)+(4-c)+c=3c+1,
∴4≤m≤13.
则m的最大值与最小值的和是4+13=17.
|
解得:
|
根据题意得:
|
解得:1≤c≤4.
则m=3a+b+c=3(c-1)+(4-c)+c=3c+1,
∴4≤m≤13.
则m的最大值与最小值的和是4+13=17.
点评:本题考查了方程组和一元一次不等式组的解,正确解关于a、b的方程组是关键.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
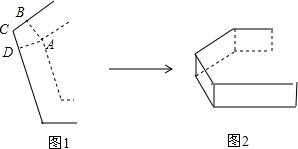 将一个正n边形的纸片(如图1)做成一个高相等且底面为正n边形的无盖纸盒,纸盒的各侧面都与底面垂直(如图2),应在正n边形的每个顶点处剪去一个四边形,如图1中的四边形ABCD是其中的一个,则∠BAD=
将一个正n边形的纸片(如图1)做成一个高相等且底面为正n边形的无盖纸盒,纸盒的各侧面都与底面垂直(如图2),应在正n边形的每个顶点处剪去一个四边形,如图1中的四边形ABCD是其中的一个,则∠BAD= 如图,已知点P是菱形ABCD的边BC上的一点,且∠PAD=∠B=80°,那么∠PDC的度为
如图,已知点P是菱形ABCD的边BC上的一点,且∠PAD=∠B=80°,那么∠PDC的度为