题目内容
8.已知△ABC∽△A′B′C,BD和B′D′是它们的对应中线,$\frac{AC}{A′C′}$=$\frac{3}{2}$,B′D′=4cm,求BD的长.分析 相似三角形对应中线的比等于相似比,即对应边的比.因而BD:B′D′=3:2解得:BD=6cm.
解答 解:∵△ABC∽△A′B′C′
∴AC:A′C′=BD:B′D′
∵$\frac{AC}{A′C′}$=$\frac{3}{2}$,B′D′=4cm
∴BD=6cm.
点评 本题考查对相似三角形性质的理解,相似三角形对应中线的比等于相似比,是需要熟记的内容.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
3.-32-|(-5)3|×(-$\frac{2}{5}$)2-18÷|-(-3)2|=( )
| A. | -51 | B. | -52 | C. | -53 | D. | -54 |
13.(1)计算:($\frac{3}{4}$-$\frac{5}{6}$+$\frac{4}{9}$)÷(-$\frac{1}{36}$)
(2)化简:3x2y-5xy2+3xy2+7x2y-2xy.
(2)化简:3x2y-5xy2+3xy2+7x2y-2xy.
18.2015年诺贝尔生理学或医学奖得主中国科学家屠呦呦,发现了一种病毒的长度约为0.00000456毫米,则数据0.00000456用科学记数法表示为( )
| A. | 0.456×10-5 | B. | 4.56×10-6 | C. | 4.56×10-7 | D. | 45.6×10-7 |
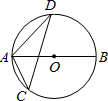 如图,AB为⊙O的直径,CD为⊙O的弦,∠ACD=52°,则∠BAD=38°.
如图,AB为⊙O的直径,CD为⊙O的弦,∠ACD=52°,则∠BAD=38°.