题目内容
如果三条线段的长x,y,z满足
,则这三条线段( )
|
| A、可构成直角三角形 |
| B、可构成钝角三角形 |
| C、可构成等边三角形 |
| D、不能构成三角形 |
考点:三角形边角关系
专题:
分析:本题可以将①变形为z=x+y-2,两边平方后代入②,得到(x-2)2+(y-2)2=0,根据非负数的性质求得x=2,y=2,再求得z=2,依此即可作出判断.
解答:解:
①变形为z=x+y-2,
两边平方为z2=(x+y-2)2,
代入②,得2xy-(x+y-2)2=4,
(x-2)2+(y-2)2=0,
则x-2=0,y-2=0,
解得x=2,y=2,
把x=2,y=2代入①,得z=2.
则x=y=z=2,
则这三条线段可构成等边三角形.
故选C.
|
①变形为z=x+y-2,
两边平方为z2=(x+y-2)2,
代入②,得2xy-(x+y-2)2=4,
(x-2)2+(y-2)2=0,
则x-2=0,y-2=0,
解得x=2,y=2,
把x=2,y=2代入①,得z=2.
则x=y=z=2,
则这三条线段可构成等边三角形.
故选C.
点评:考查了三角形边角关系,解题的关键是根据非负数的性质求得x,y,z的值,同时考查了等边三角形的判定.

练习册系列答案
相关题目
锐角三角形△ABC中,∠C=2∠B,则∠B的范围是( )
| A、10°<∠B<20° |
| B、20°<∠B<30° |
| C、30°<∠B<45° |
| D、45°<∠B<60° |
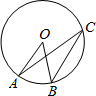 如图,点O是⊙O的圆心,点A、B、C在⊙O上,AO∥BC,∠AOB=40°,则∠OAC的度数等于( )
如图,点O是⊙O的圆心,点A、B、C在⊙O上,AO∥BC,∠AOB=40°,则∠OAC的度数等于( )| A、40° | B、60° |
| C、50° | D、20° |
