题目内容
2．古希腊数学家把数1，3，6，10，15，21，…叫做三角数，它有一定的规律性．若把第一个三角数记为a1，第二个三角数记为a2，…，第n个三角数记为an，则an-1+an=（ ）（ ）| A． | （n-1）2 | B． | n2 | C． | （n+1）2 | D． | （n+2）2 |
分析 先求出：a1+a2=4=22，a2+a3=9=32，a3+a4=16=42，a4+a5=25=52，…根据规律可以写出an-1+an的结果．
解答 解：∵a1+a2=4=22，
a2+a3=9=32，
a3+a4=16=42，
a4+a5=25=52，
…
∴an-1+an=n2，
故选B．
点评 本题考查规律型：数字的变化类问题，解题的关键是学会从一般到特殊的探究方法，找到规律后即可解决问题属于中考常考题型．
练习册系列答案
相关题目
10．
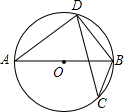如图，AB是⊙O的直径，CD是⊙O的弦，连接AD、DB、BC，若∠ABD=55°，则∠BCD的度数为（ ）
如图，AB是⊙O的直径，CD是⊙O的弦，连接AD、DB、BC，若∠ABD=55°，则∠BCD的度数为（ ）| A． | 65° | B． | 55° | C． | 45° | D． | 35° |
17．下列不等式组无解的是（ ）
| A． | $\left\{\begin{array}{l}{x+1＜0}\\{x-2＞0}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{x-1＜0}\\{x+2＞0}\end{array}\right.$ | C． | $\left\{\begin{array}{l}{x+1＞0}\\{x-2＞0}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{x-2＜0}\\{x+1＜0}\end{array}\right.$ |
7．下列运算正确的是（ ）
| A． | $\sqrt{4}$=±2 | B． | 2+$\sqrt{3}$=2$\sqrt{3}$ | C． | 2x-2=$\frac{1}{2{x}^{2}}$ | D． | （-a3）2=a6 |
14．
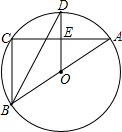如图，AB是△ABC的外接圆⊙O的直径，D为⊙O上一点，OD⊥AC，垂足为E，BC=5，AE=6，则DE的长为（ ）
如图，AB是△ABC的外接圆⊙O的直径，D为⊙O上一点，OD⊥AC，垂足为E，BC=5，AE=6，则DE的长为（ ）| A． | 4$\sqrt{2}$ | B． | 3$\sqrt{3}$ | C． | 4 | D． | $\frac{7}{2}$ |
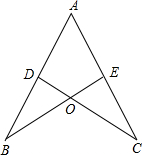如图，AB=AC，CD⊥AB于D，BE⊥AC于E，BE与CD相交于点O．