题目内容
20.某公司投资40万元生产A,B两种产品.已知投资A产品获得的利润y1(万元)与投资金额x(万元)的关系为y1=x;投资B产品获得的利润y2(万元)与投资金额x(万元)的关系为y2=$\frac{1}{10}$x2,且投资B产品的金额不少于A产品的投资金额.但不多于A产品投资金额的3倍.设投资B产品的金额为x万元.(1)若公司计划获得60万元的总利润,求出投资A,B两种产品各多少万元?
(2)求出公司获得的总利润W(万元)与x的函数关系式,并写出x的取值范围;
(3)当投资B产品的金额为多少万元时,该公司获得的利润最大,并求出最大利润.
分析 (1)根据题意列方程x+$\frac{1}{10}$x2=60,解方程即可;
(2)由题意得解不等式0≤x≤$\frac{1}{10}{x}^{2}$≤3x,求出x取值范围,根据总利润等于A,B两种产品利润之和,即可求出解析式;
(3)先求出对称轴,由于a>0,在对称轴右侧,函数随x增大而最大,把x的最大值代入即可.
解答 (1)由题意得:x+$\frac{1}{10}$x2=60,解得:x1=20,x2=-30(舍去),
∴投资B产品各20万元,投资A种产品40-20=20(万元);
(2)由题意得:0≤x≤$\frac{1}{10}{x}^{2}$≤3x,
解得:10≤x≤30,
∴w=y1+y2=$\frac{1}{10}$x2+x(10≤x≤30);
(3)x=-$\frac{1}{2×\frac{1}{10}}$=-5,
在对称轴右侧,w随x增大而增大,
∴当x=30时,w最大,最大值为w=$\frac{1}{10}$×302+30=120,
∴投资B产品的金额为30万元时,该公司获得的利润最大,最大利润为120万元.
点评 本题主要考查了方程,不等式,列函数解析式,求函数最值问题,能根据题意求出自变量取值范围是解决问题的关键.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
10.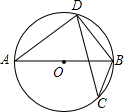 如图,AB是⊙O的直径,CD是⊙O的弦,连接AD、DB、BC,若∠ABD=55°,则∠BCD的度数为( )
如图,AB是⊙O的直径,CD是⊙O的弦,连接AD、DB、BC,若∠ABD=55°,则∠BCD的度数为( )
 如图,AB是⊙O的直径,CD是⊙O的弦,连接AD、DB、BC,若∠ABD=55°,则∠BCD的度数为( )
如图,AB是⊙O的直径,CD是⊙O的弦,连接AD、DB、BC,若∠ABD=55°,则∠BCD的度数为( )| A. | 65° | B. | 55° | C. | 45° | D. | 35° |
8. 如图是正方体的一个平面展开图,如果原正方体上“友”所在的面为前面,则“信”与“国”所在的面分别位于( )
如图是正方体的一个平面展开图,如果原正方体上“友”所在的面为前面,则“信”与“国”所在的面分别位于( )
 如图是正方体的一个平面展开图,如果原正方体上“友”所在的面为前面,则“信”与“国”所在的面分别位于( )
如图是正方体的一个平面展开图,如果原正方体上“友”所在的面为前面,则“信”与“国”所在的面分别位于( )| A. | 上,下 | B. | 右,后 | C. | 左,右 | D. | 左,后 |
5.下列计算正确的是( )
| A. | (a3)2=a5 | B. | a3+a2=a5 | C. | a5÷a2=a3 | D. | ($\frac{x}{2}$)3=$\frac{{x}^{3}}{2}$ |
10.将代数式x2+6x-3化为(x+p)2+q的形式,正确的是( )
| A. | (x+3)2+6 | B. | (x-3)2+6 | C. | (x+3)2-12 | D. | (x-3)2-12 |
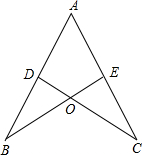 如图,AB=AC,CD⊥AB于D,BE⊥AC于E,BE与CD相交于点O.
如图,AB=AC,CD⊥AB于D,BE⊥AC于E,BE与CD相交于点O.