题目内容
12.已知正方形ABCD和正方形OEFG的位置如图所示,且它们的边长均为2cm,OE、OG分别与对角线的一半OB、OC重合,则图(1)中的重合面积是多少?若正方形OEFG绕点O顺时针旋转一个角度α,则得到如图(2)所示图形,则图(2)中阴影部分的面积又是多少?请给予合理的解释.
分析 图1中的重合部分面积等于正方形面积的$\frac{1}{4}$,连接OC、OB,AB与OE交于点N,BC与OG交于点M,通过全等三角形证明这个重合部分的面积等于正方形面积的$\frac{1}{4}$.
解答 解:在图1中,∵四边形ABCD是正方形,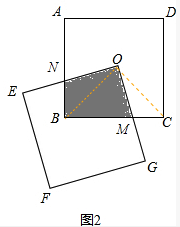
∴OA=OC=OB=OD,
∴S△BOC=$\frac{1}{4}$S正方形ABCD=$\frac{1}{4}$×4=1,
在图2中,连接OC、OB,AB与OE交于点N,BC与OG交于点M.
∵∠MON=∠BOC=90°,
∴∠NOB=∠COM,
在△COM和△BON中,
$\left\{\begin{array}{l}{∠COM=∠BON}\\{OC=OB}\\{∠OCM=∠OBN}\end{array}\right.$,
∴△OCM≌△OBN,
∴S△OCM=S△OBN,
∴S四边形OMBN=S△OBC=$\frac{1}{4}$S正方形ABCD=1.
点评 本题考查正方形的性质、全等三角形的判定和性质,学会把求不规则图形面积转化为规则图形面积,构造全等三角形是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.下列图形中,既是轴对称又是中心对称的图形是( )
| A. | 平行四边形 | B. | 等腰梯形 | C. | 等边三角形 | D. | 圆 |
2.已知等腰三角形的一边长等于4,一边长等于9,则它的周长为( )
| A. | 22 | B. | 17 | C. | 17或22 | D. | 26 |
 如图,抛物线y=ax2+bx+c的图象与x轴交于A、B两点,与y轴交于点C,其中点B在x轴的正半轴上,点C在y轴的正半轴上,线段OA、OC的长(OA<OC)是方程x2-4x+3=0的两个根,且抛物线的对称轴是直线x=1.
如图,抛物线y=ax2+bx+c的图象与x轴交于A、B两点,与y轴交于点C,其中点B在x轴的正半轴上,点C在y轴的正半轴上,线段OA、OC的长(OA<OC)是方程x2-4x+3=0的两个根,且抛物线的对称轴是直线x=1. 如图,AC与BD交于点O,AB∥DC,AB=DC.
如图,AC与BD交于点O,AB∥DC,AB=DC. 如图,在平面直角坐标系中,将直角三角形的直角顶点放在点P(4,4)处,两直角边与坐标轴交于点A和点B.
如图,在平面直角坐标系中,将直角三角形的直角顶点放在点P(4,4)处,两直角边与坐标轴交于点A和点B.