题目内容
6. 如图,将Rt△ABC绕直角顶点C按顺时针旋转90°到△DEC的位置,已知斜边AB=10cm,BC=6cm.设DE的中点为M,连接AM,则AM的长为( )
如图,将Rt△ABC绕直角顶点C按顺时针旋转90°到△DEC的位置,已知斜边AB=10cm,BC=6cm.设DE的中点为M,连接AM,则AM的长为( )| A. | 4 | B. | 5 | C. | 6 | D. | $\sqrt{41}$ |
分析 首先过点M作MF⊥EC于点F,结合旋转的性质进而结合三角形中位线的性质得出FM,AF的长,进而利用勾股定理得出AM的长.
解答 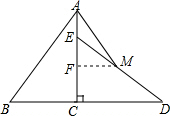 解:如图所示:过点M作MF⊥EC于点F,
解:如图所示:过点M作MF⊥EC于点F,
∵斜边AB=10cm,BC=6cm,
∴AC=8cm,
∵将Rt△ABC绕直角顶点C按顺时针旋转90°到△DEC的位置,
∴AC=CD=8cm,EC=BC=6cm,
∵DE的中点为M,MF⊥EC,
∴EF=FC=3cm,
∴FM=$\frac{1}{2}$DC=4cm,AF=5cm,
∴AM=$\sqrt{A{F}^{2}+F{M}^{2}}$=$\sqrt{{5}^{2}{+4}^{2}}$=$\sqrt{41}$(cm).
故选:D.
点评 此题主要考查了旋转的性质以及勾股定理和三角形中位线的性质等知识,正确得出AF的长是解题关键.

练习册系列答案
相关题目
16.若分式方程$\frac{ax+1}{2x-1}$=1有解,则a的值是( )
| A. | a≠-2 | B. | a≠0 | C. | a≠2且a≠-2 | D. | a≠0或a≠-2 |
17.下列方程组中是二元一次万程组的是( )
| A. | $\left\{\begin{array}{l}{xy=1}\\{x+y=2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{5x-2y=1}\\{\frac{1}{x}+y=3}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{2x+z=0}\\{3x-y=\frac{1}{5}}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+\frac{y}{2}=5}\\{\frac{x}{2}+\frac{y}{3}=7}\end{array}\right.$ |
11.已知⊙O的半径为3cm,点P是直线l上一点,OP的长为4cm,则直线l与⊙O的位置关系是( )
| A. | 相交 | B. | 相切 | ||
| C. | 相离 | D. | 以上三种都有可能 |
18.下列各图中,是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
16.下列运算有错误的是( )
| A. | 2-7=(+2)+(-7) | B. | (-5)÷(-$\frac{1}{2}$)=-5×(-2) | C. | 7x-(x+1)=7x-x-1 | D. | 3(x+8)=3x+8 |
 如图,某油田有四个油井分别位于A,B,C,D四个点上,如果要建一个维修站H,使这个维修站到这四个油井的距离之和最短,那么这个维修站就必须建于AC,BD的交点上,知道这是为什么吗?
如图,某油田有四个油井分别位于A,B,C,D四个点上,如果要建一个维修站H,使这个维修站到这四个油井的距离之和最短,那么这个维修站就必须建于AC,BD的交点上,知道这是为什么吗? 如图,直角△ACD中,B为AD延长线上一点,且满足AB=CD,在CD上的一点E满足DE=DB,连接BE,F为BE中点,延长AF与过B点的DC的平行线交于点G,连接CG,求证:∠CAG=45°,AD+BG=CG.
如图,直角△ACD中,B为AD延长线上一点,且满足AB=CD,在CD上的一点E满足DE=DB,连接BE,F为BE中点,延长AF与过B点的DC的平行线交于点G,连接CG,求证:∠CAG=45°,AD+BG=CG.