题目内容
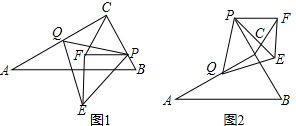
14.如图1,在Rt△ABC中,∠ACB=90°,∠A=30°,P为BC边上任意一点,点Q为AC边动点,分别以CP、PQ为边做等边△PCF和等边△PQE,连接EF.(1)证明:CQ=EF;
(2)试探索EF与AB位置关系,并说明理由;
(3)如图2,当点P为BC延长线上任意一点时,结论(2)是否成立?请说明理由.
分析 (1)根据等边三角形的性质和SAS证明△PEF与△CQP全等即可;
(2)通过等边三角形的性质(三条边相等、三个角相等)求得PF=PC,PE=PQ,∠EPF=∠QPC;然后根据全等三角形的判定定理SAS证明△PFE≌△PCQ,再根据全等三角形的性质(对应角相等)知∠EPF=∠QPC=90°;接下来由平行线的判定定理(同位角相等,两直线平行)知PF∥AB;最后由平行线的性质(两平行线中,有一条垂直于第三条直线,则另一条也垂直于第三条直线)知EF⊥AB;
(3)通过等边三角形的性质(三条边相等、三个角相等)求得PF=PC,PE=PQ,∠EPF=∠QPC;然后根据全等三角形的判定定理SAS证明△PFE≌△PCQ,再根据全等三角形的性质(对应角相等)知∠EPF=∠QPC=90°;接下来由平行线的判定定理(内错角相等,两直线平行)知PF∥AB;最后由平行线的性质(两平行线中,有一条垂直于第三条直线,则另一条也垂直于第三条直线)知EF⊥AB.
解答 证明:(1)∵△PCF和△PQE都是等边三角形,
∴PF=PC,PE=PQ,
∠EPF+∠EPC=∠QPC+∠EPC=60°,
∴∠EPF=∠QPC,
在△PFE和△PCQ中
$\left\{\begin{array}{l}{PF=PC}\\{∠EPF=∠QPC}\\{PE=PQ}\end{array}\right.$,
∴△PFE≌△PCQ(SAS);
∴CQ=EF;
(2)EF⊥AB,理由如下:
∵△PCF和△PQE都是等边三角形,
∴PF=PC,PE=PQ,
∠EPF+∠FPQ=∠QPC+∠FPQ=60°,
∴∠EPF=∠QPC,
在△PFE和△PCQ中
$\left\{\begin{array}{l}{PF=PC}\\{∠EPF=∠QPC}\\{PE=PQ}\end{array}\right.$,
∴△PFE≌△PCQ(SAS);
∴∠EFP=∠QCP=90°,
∴EF⊥PF;
在Rt△ABC中,∠ACB=90°,∠A=30°,
∴∠B=60°;
又∵∠FPC=60°,
∴∠B=∠FPC,
∴PF∥AB(同位角相等,两直线平行),
∴EF⊥AB;
(3)当点P为BC延长线上任意一点时,(2)结论成立.
∵△PCF和△PQE都是等边三角形,
∴PF=PC,PE=PQ,
∠EPF+∠EPC=∠QPC+∠EPC=60°,
∴∠EPF=∠QPC,
在△PFE和△PCQ中
$\left\{\begin{array}{l}{PF=PC}\\{∠EPF=∠QPC}\\{PE=PQ}\end{array}\right.$,
∴△PFE≌△PCQ(SAS);
∴∠EFP=∠QCP=90°,
∴EF⊥PF;
在Rt△ABC中,∠ACB=90°,∠A=30°,
∴∠B=60°;
又∵∠FPC=60°,
∴∠B=∠FPC,
∴PF∥AB(内错角相等,两直线平行),
∴EF⊥AB.
点评 本题综合考查了全等三角形的性质、全等三角形的判定与性质.解答本题要充分利用等边三角形的三边关系、三角关系,可有助于提高解题速度和准确率.

 名校课堂系列答案
名校课堂系列答案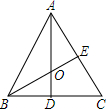 已知:等边△ABC中,AD⊥BC,BE⊥AC,垂足分别为点D、E,AD与BE交于O.求证:AO=2OD.
已知:等边△ABC中,AD⊥BC,BE⊥AC,垂足分别为点D、E,AD与BE交于O.求证:AO=2OD.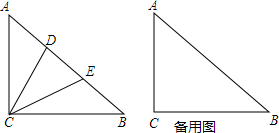
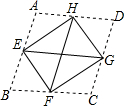 如图,将菱形ABCD的四个角沿相邻两边中点的连线向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH,已知EH=8cm,EF=6cm.
如图,将菱形ABCD的四个角沿相邻两边中点的连线向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH,已知EH=8cm,EF=6cm.
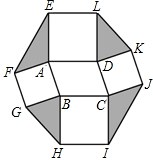 如图,以?ABCD的四条边为边,分别向外作正方形,连结EF,GH,IJ,KL.如果?ABCD的面积为8,则图中阴影部分四个三角形的面积和为( )
如图,以?ABCD的四条边为边,分别向外作正方形,连结EF,GH,IJ,KL.如果?ABCD的面积为8,则图中阴影部分四个三角形的面积和为( )