题目内容
2.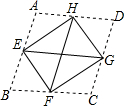 如图,将菱形ABCD的四个角沿相邻两边中点的连线向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH,已知EH=8cm,EF=6cm.
如图,将菱形ABCD的四个角沿相邻两边中点的连线向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH,已知EH=8cm,EF=6cm.(1)探究四边形EFGH是什么特殊四边形?并予以证明.
(2)求AD的长.
分析 (1)根据折叠的性质推知∠1=∠2,∠3=∠4,则根据邻补角的定义易求∠HEF=90°.同理推知四边形EFGH的其它三个内角都是90°,得证;
(2)先由勾股定理求出HF=10cm,根据矩形的对角线相等得出EG=HF=10cm.再证明四边形AEGD是平行四边形,根据平行四边形的对边相等得出AD=EG=10cm.
解答 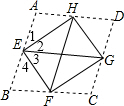 (1)证明:如图,由折叠的性质可知:∠1=∠2,∠3=∠4,
(1)证明:如图,由折叠的性质可知:∠1=∠2,∠3=∠4,
∵∠1+∠2+∠3+∠4=180°,
∴2∠2+2∠3=180°,即∠2+∠3=90°,
∴∠HEF=90°,
同理可得:∠EFG=90°,∠FGH=90°,∠EHG=90°,
∴四边形EFGH是矩形;
(2)解:∵∠HEF=90°,EH=8cm,EF=6cm,
∴HF=10cm.
∵四边形EFGH是矩形,
∴EG=HF=10cm.
∵菱形ABCD中,AB=CD,AB∥CD,
∵E,G分别是AB,CD中点,
∴AE=DG,AE∥DG,
∴四边形AEGD是平行四边形,
∴AD=EG=10cm.
点评 本题考查了菱形的性质,矩形的判定与性质,平行四边形的判定与性质以及折叠问题.折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.

练习册系列答案
相关题目
12.若△ABC∽△DEF,且面积比为1:3,则△ABC与△DEF的周长比为( )
| A. | 1:3 | B. | 1:9 | C. | 1:$\sqrt{3}$ | D. | 3:1 |
13.若x=2是方程2a-3x=6的解,则a的值是( )
| A. | $\frac{1}{2}$ | B. | -4 | C. | $\frac{2}{3}$ | D. | 6 |
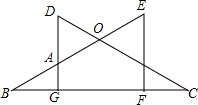 如图,已知CD=BE,DG⊥BC于点G,EF⊥BC于点F,且DG=EF.
如图,已知CD=BE,DG⊥BC于点G,EF⊥BC于点F,且DG=EF.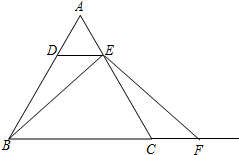 如图,已知在△ABC中,AB=AC,点D、E分别在边AB、AC上,且AD=AE.
如图,已知在△ABC中,AB=AC,点D、E分别在边AB、AC上,且AD=AE. 一个小立方块的六个面分别标有数字1,2,3,4,5,6,从三个不同方向看到的情形如图所示,则如图放置时三个底面上的数字之和等于(
一个小立方块的六个面分别标有数字1,2,3,4,5,6,从三个不同方向看到的情形如图所示,则如图放置时三个底面上的数字之和等于(