题目内容
4.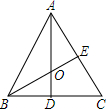 已知:等边△ABC中,AD⊥BC,BE⊥AC,垂足分别为点D、E,AD与BE交于O.求证:AO=2OD.
已知:等边△ABC中,AD⊥BC,BE⊥AC,垂足分别为点D、E,AD与BE交于O.求证:AO=2OD.
分析 根据全等三角形的判定和性质进行证明即可.
解答 证明:∵等边△ABC中AD⊥BC,BE⊥AC,
∴∠BAE=60°,
∴2AE=AB,
同理可得:2BD=AB,2OD=OB,
在△AOE与△OBD中,
$\left\{\begin{array}{l}{∠BOD=∠AOE}\\{∠ODB=∠OEA=90°}\\{BD=AE}\end{array}\right.$,
∴△AOE≌△OBD(AAS),
∴AO=OB,
∴AO=2OD.
点评 此题考查三角形重心问题,关键是根据全等三角形的判定和性质得出AO=2OD.

练习册系列答案
相关题目
12.若△ABC∽△DEF,且面积比为1:3,则△ABC与△DEF的周长比为( )
| A. | 1:3 | B. | 1:9 | C. | 1:$\sqrt{3}$ | D. | 3:1 |
19.若am=5,an=3,则am+n的值为( )
| A. | 15 | B. | 25 | C. | 35 | D. | 45 |
9.下列说法:
①0是绝对值最小的有理数;
②相反数大于本身的数是负数;
③有理数分为正数和负数;
④有理数都可以用数轴上的点表示.
其中正确的是( )
①0是绝对值最小的有理数;
②相反数大于本身的数是负数;
③有理数分为正数和负数;
④有理数都可以用数轴上的点表示.
其中正确的是( )
| A. | ①②③ | B. | ①③④ | C. | ①②④ | D. | ②③④ |
13.若x=2是方程2a-3x=6的解,则a的值是( )
| A. | $\frac{1}{2}$ | B. | -4 | C. | $\frac{2}{3}$ | D. | 6 |