题目内容
9.如图(甲),∠AOC和∠BOD都是直角.(1)如果∠DOC=30°,∠AOB的度数是150度;
(2)找出图(甲)中和∠AOD相等的角,并说明相等的理由.
(3)在图(乙)中利用能够画直角的工具再画一个与∠BOC相等的角.(请写出图中所画的直角,并写出与∠BOC相等的角).

分析 (1)根据∠AOC=90°,∠DOC=30°,求出∠AOD的度数,然后即可求出∠AOB的度数;
(2)根据余角的性质可得图(甲)中和∠AOD相等的角;
(3)首先以OB为边,在∠BOC外画∠BOD=90°,再以OC为边在∠COD外画∠AOC=90°,即可得到∠AOD=∠BOC.
解答 解:(1)∵∠AOC=∠DOB=90°,∠DOC=30°,
∴∠AOD=90°-30°=60°,
∴∠AOB=90°+60°=150°.
(2)图(甲)中和∠AOD相等的角是∠BOC,同角的余角相等(或见下面解释)
∵∠AOC=∠DOB=90°,
∴∠AOD+∠DOC=∠BOC+∠DOC,
∴∠AOD=∠BOC;
(3)如图所示:∠AOD=∠BOC.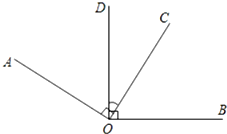
故答案为:150.
点评 本题考查了余角和补角,以及角的计算,解决本题的关键是熟记余角和补角的定义.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
19.若am=5,an=3,则am+n的值为( )
| A. | 15 | B. | 25 | C. | 35 | D. | 45 |
20.下列计算中正确的是( )
| A. | (-3x3y3)2=3x6y6 | B. | a10•a2=a20 | ||
| C. | (-m2)5•(-m3)2=m16 | D. | (-$\frac{1}{2}$x2y4)3=-$\frac{1}{8}$x6y12 |
4.小敏到距家1500米的学校去上学,小敏出发10分钟后,小敏的爸爸立即去追小敏,且在距离学校60米的地方追上了她.已知爸爸比小敏的速度快100米/分,求小敏的速度.若设小敏的速度为x米/分,则根据题意所列方程正确的是( )
| A. | $\frac{1440}{x}=\frac{1440}{x+100}+10$ | B. | $\frac{1440}{x-100}-\frac{1440}{x}=10$ | ||
| C. | $\frac{1440}{x}=\frac{1440}{x-100}+10$ | D. | $\frac{1440}{x+100}-\frac{1440}{x}=10$ |
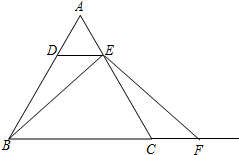 如图,已知在△ABC中,AB=AC,点D、E分别在边AB、AC上,且AD=AE.
如图,已知在△ABC中,AB=AC,点D、E分别在边AB、AC上,且AD=AE.
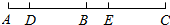 如图,线段AC上依次有D,B,E三点,其中点B为线段AC的中点,AD=BE=$\frac{1}{5}$AE,若DB=12.
如图,线段AC上依次有D,B,E三点,其中点B为线段AC的中点,AD=BE=$\frac{1}{5}$AE,若DB=12.