题目内容
9.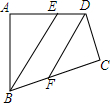 如图,在四边形ABCD中,∠A=∠C=90°,BE平分∠ABC,DF平分∠ADC,BE与DF有怎样的位置关系?为什么?
如图,在四边形ABCD中,∠A=∠C=90°,BE平分∠ABC,DF平分∠ADC,BE与DF有怎样的位置关系?为什么?
分析 根据角平分线的定义和四边形的内角和进行解答即可.
解答 解:BE∥DF,理由如下:
∵在四边形ABCD中,∠A=∠C=90°,
∴∠ABC+∠ADC=180°,
∵BE平分∠B,DF平分∠D,
∴∠EBF+∠FDC=90°,
∵∠C=90°,
∴∠DFC+∠FDC=90°,
∴∠EBF=∠DFC,
∴BE∥DF.
点评 此题考查平行线的判定,关键是根据角平分线的定义和四边形的内角和进行解答.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
4.
| 计算: (1)28+(-72) | (2)0+(-5) | (3)-$\frac{1}{5}$+(+$\frac{1}{6}$) |
| (4)(-3)-(-5) | (5)$({-3\frac{1}{2}})-5\frac{1}{4}$ | (6)(-8)+(-5)-(+5) |
| (7)-37-40+3-22 | (7)$(({-4})×({-\frac{3}{4}})×2$ | (8)(-5)×(-4)×3×(-2) |
| (9)-12÷$\frac{1}{4}÷({-\frac{8}{3}})$ | (10)$({\frac{1}{3}-\frac{5}{6}+\frac{7}{9}})÷({\frac{1}{18}})$ | (11)9$\frac{15}{16}×({-8})$ |
| (12)100÷$\frac{1}{8}×({-8})$ | (13)$1÷({-\frac{2}{7}})×\frac{1}{7}$ | (14)$\frac{1}{2}×({-\frac{4}{15}})÷\frac{2}{3}$. |
14.一个不透明的袋子中有2个白球,1个黄球和1个红球,这些球除颜色不同外其他完全相同,若从袋子中随机摸出1个球后,放回摇匀,再取出1个球,则两次取出都是白球的概率为( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
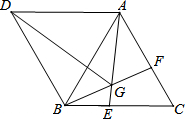 如图,△ABC与△ABD都是等边三角形,点E,F分别在BC,AC上,BE=CF,AE与BF交于点G.
如图,△ABC与△ABD都是等边三角形,点E,F分别在BC,AC上,BE=CF,AE与BF交于点G. △ABC中,AB=AC,AD是△ABC的中线,BF垂直AC于F交AD于E,连接CE交AB于点G,求证:CG⊥AB.
△ABC中,AB=AC,AD是△ABC的中线,BF垂直AC于F交AD于E,连接CE交AB于点G,求证:CG⊥AB.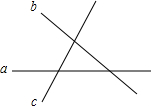 如图,直线a、b、c表示三条公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有4处.
如图,直线a、b、c表示三条公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有4处.