题目内容
14.一个不透明的袋子中有2个白球,1个黄球和1个红球,这些球除颜色不同外其他完全相同,若从袋子中随机摸出1个球后,放回摇匀,再取出1个球,则两次取出都是白球的概率为( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
分析 列举出所有情况,看两次都摸到白球的情况数占总情况数的多少即可.
解答 解:画树形图得:
共有16种等可能的结果数,其中两个都是白球的占4种,
所以两次都摸到白球的概率=$\frac{4}{16}$=$\frac{1}{4}$.
故选B.
点评 此题考查的是用列表法或树状图法求概率.列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;解题时要注意此题是放回实验还是不放回实验.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
19.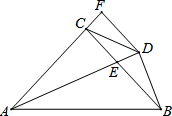 如图,在△ABC中,AC=BC,∠ACB=90°,AE平分∠BAC交BC于E,BD⊥AE于 D,DF⊥AC交AC的延长线于F,连接CD,给出三个结论:
如图,在△ABC中,AC=BC,∠ACB=90°,AE平分∠BAC交BC于E,BD⊥AE于 D,DF⊥AC交AC的延长线于F,连接CD,给出三个结论:
①AE=2BD;②AB-AC=CE;③CE=2FC;
其中正确的结论有( )
 如图,在△ABC中,AC=BC,∠ACB=90°,AE平分∠BAC交BC于E,BD⊥AE于 D,DF⊥AC交AC的延长线于F,连接CD,给出三个结论:
如图,在△ABC中,AC=BC,∠ACB=90°,AE平分∠BAC交BC于E,BD⊥AE于 D,DF⊥AC交AC的延长线于F,连接CD,给出三个结论:①AE=2BD;②AB-AC=CE;③CE=2FC;
其中正确的结论有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
6.已知-1是关于x的一元二次方程x2+x-a=0的一个根,则a的值是( )
| A. | 3 | B. | 2 | C. | -1 | D. | 0 |
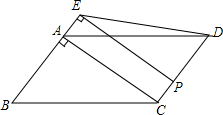 如图,在?ABCD中,在AB=3,BC=5,对角线AC⊥AB.点P从点D出发,沿折线DC-CB以每秒1个单位长度的速度向终点B运动(不与点B、D重合),过点P作PE⊥AB,交射线BA于点E,连结PD、DE.设点P的运动时间为t(秒),△PDE与?ABCD重叠部分图形的面积为S(平方单位).
如图,在?ABCD中,在AB=3,BC=5,对角线AC⊥AB.点P从点D出发,沿折线DC-CB以每秒1个单位长度的速度向终点B运动(不与点B、D重合),过点P作PE⊥AB,交射线BA于点E,连结PD、DE.设点P的运动时间为t(秒),△PDE与?ABCD重叠部分图形的面积为S(平方单位).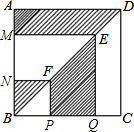 正方形ABCD的边长为2,点E、F分别是对角线BD上的两点,过点E、F分别作AD、AB的平行线,如图所示,则图中阴影部分的面积之和等于2.
正方形ABCD的边长为2,点E、F分别是对角线BD上的两点,过点E、F分别作AD、AB的平行线,如图所示,则图中阴影部分的面积之和等于2.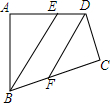 如图,在四边形ABCD中,∠A=∠C=90°,BE平分∠ABC,DF平分∠ADC,BE与DF有怎样的位置关系?为什么?
如图,在四边形ABCD中,∠A=∠C=90°,BE平分∠ABC,DF平分∠ADC,BE与DF有怎样的位置关系?为什么?